生物工学演習D -第4回- 電気回路の微分方程式モデル
今回の目標
□電気回路の微分方程式を立てる方法を理解する
□電気回路の微分方程式モデルの解や伝達関数をラプラス変換を用いて求める方法を理解する
電気回路の微分方程式モデル
主な構成要素
・電源
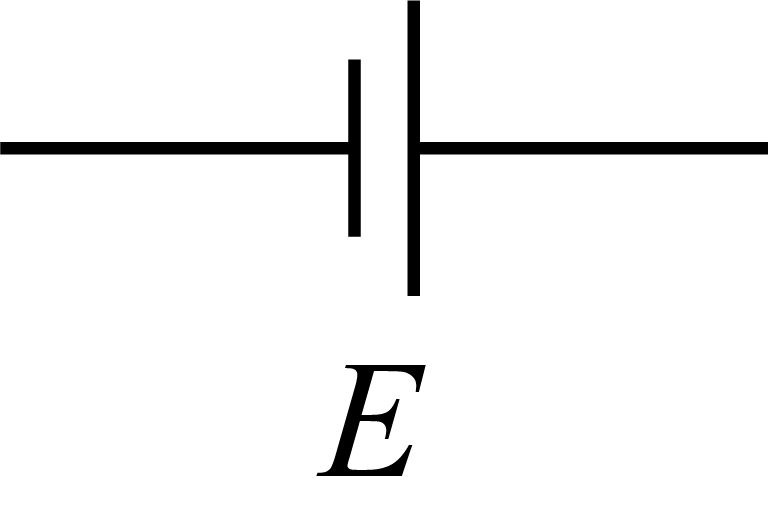
\begin{align}
E
\end{align}
・抵抗\(R\):単位(\(\mathrm{\Omega}\),オーム)

\begin{align}
E(t)=Ri(t)
\end{align}
・コンデンサー\(C\):単位(\(\mathrm{F}\),ファラド)
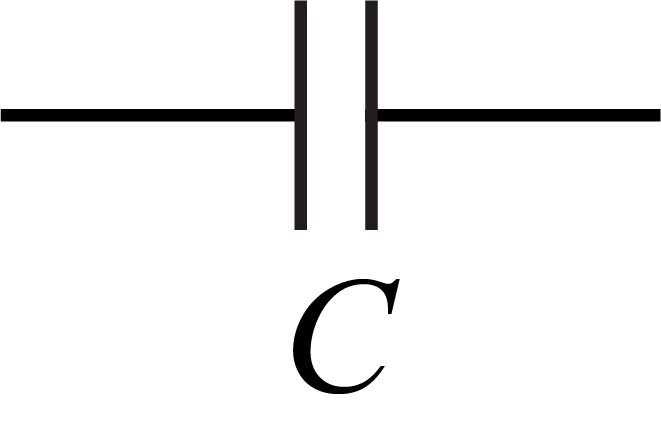
\begin{align}
E(t)&=\frac{1}{C}\int_{-\infty}^ti(t’)dt’\\
E(t)&=\frac{1}{C}\int_{0}^ti(t’)dt’ + \frac{1}{C}\int_{-\infty}^0i(t’)dt’
\end{align}
ここで
\begin{align}
\int_{-\infty}^0i(t’)dt’ = q_\mathrm{c}(0) = CV_\mathrm{c}(0)
\end{align}
\(t=0\)でコンデンサに電荷がたまっていないとき\(q_\mathrm{c}(0)=0\)
・コイル\(L\):単位(\(\mathrm{H}\),ヘンリー)
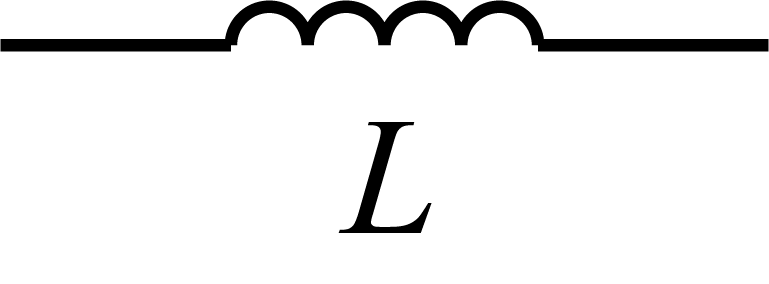
\begin{align}
E(t)=L\frac{d}{dt}i(t)
\end{align}
電気回路を支配する法則
電気回路では電流と電圧についてそれぞれ2つの法則がある.
キルヒホッフの第一法則:接続点に流出入する電流の総和がゼロ
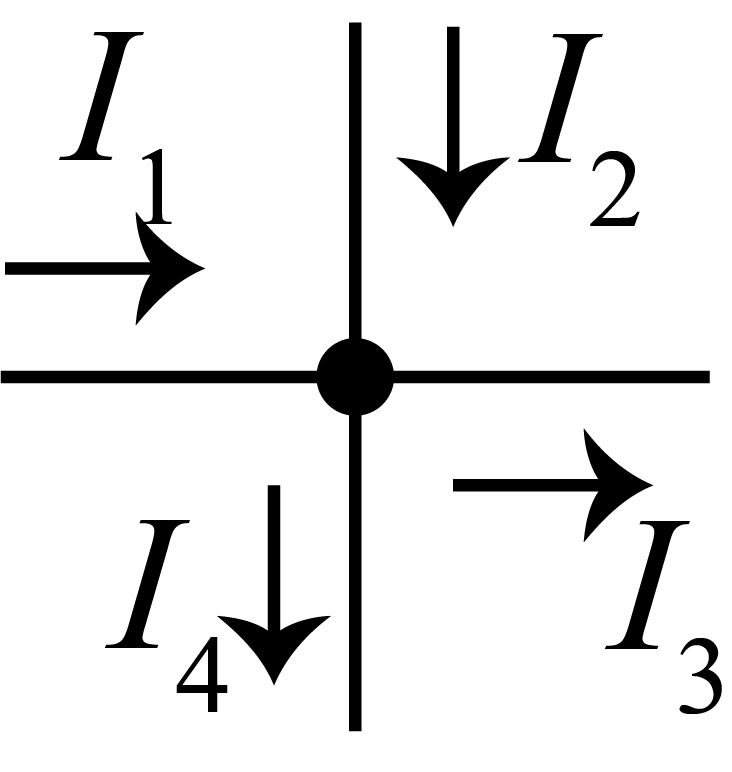
この例の場合
\begin{align}
I_1 + I_2 = I_3 + I_4
\end{align}
キルヒホッフの第二法則:電圧降下の総和がゼロ
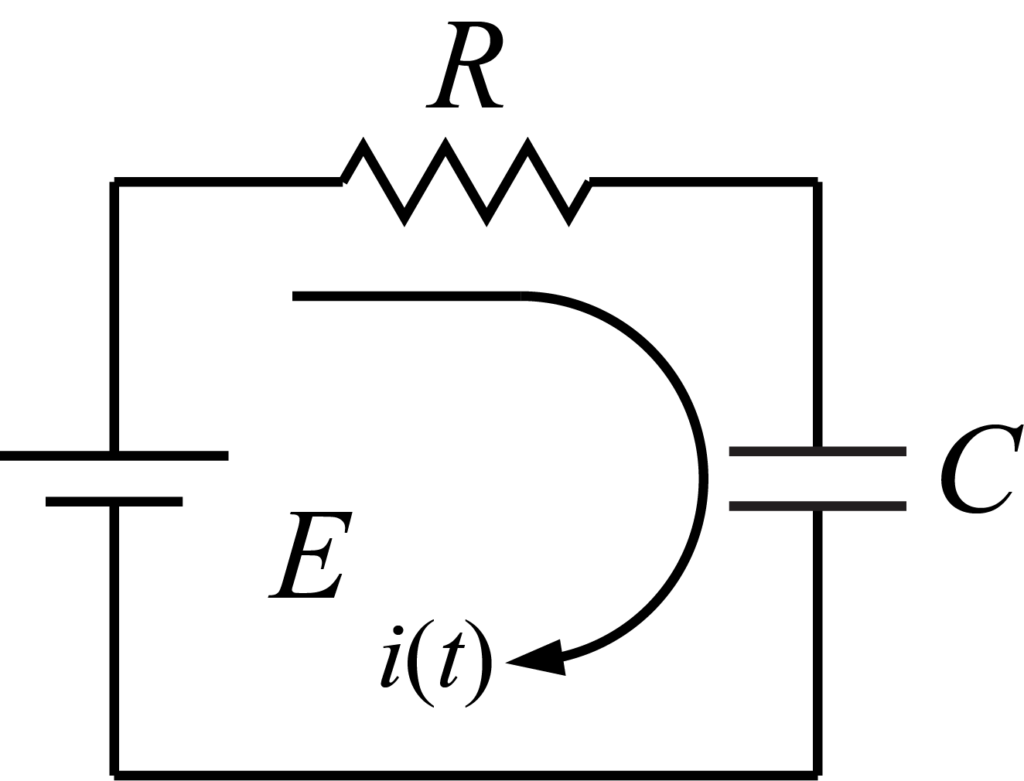
この例の場合
\begin{align}
E – Ri(t) – \frac{1}{C}\int_0^t i(t’) dt’ = 0
\end{align}
電気回路の微分方程式モデルの立て方
例題1
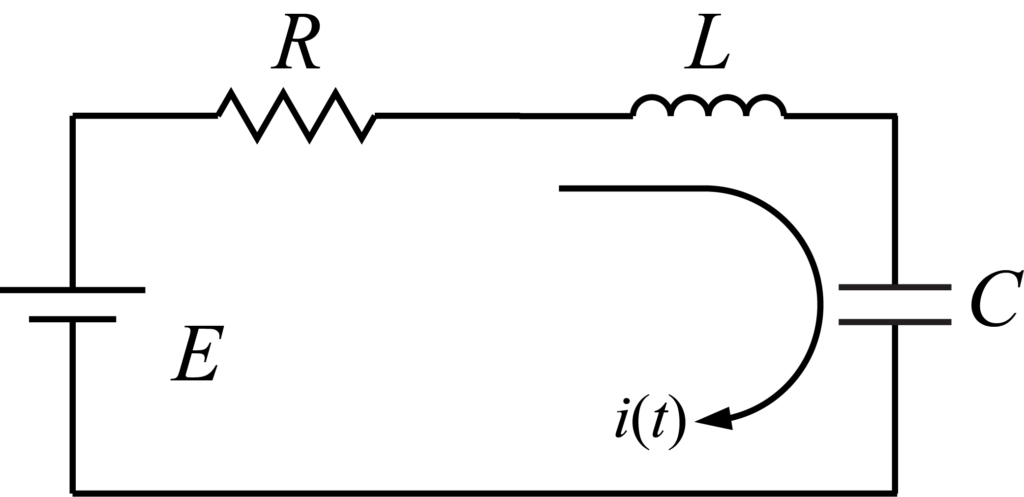
キルヒホッフの第二法則より
\begin{align}
E – Ri(t) – L\frac{d}{dt}i(t) – \frac{1}{C}\int_0^t i(t’) dt’ = 0
\end{align}
例題2

スイッチを入れた状態を考えると
キルヒホッフの第二法則より
\begin{align}
E = \frac{1}{C}\int_0^t i_1(t’) dt’ = Ri_2(t) – L\frac{d}{dt}i_2(t)
\end{align}
また,キルヒホッフの第一法則より
\begin{align}
i_1(t) + i_2(t) = i(t)
\end{align}
解\(i(t)\)の求め方
例題2にて\(t=0\)にてスイッチを入れた時の電流の時間変化\(i(t)\)を求める.
上式をそれぞれラプラス変換すると
\begin{align}
\frac{E}{s} &= \frac{1}{Cs}I_1(s) = RI_2(s) – LsI_2(s)\\
I_1(s) + I_2(s) &= I(s)
\end{align}
\(I_1(s)\)と\(I_2(s)\)を消すと
\begin{align}
I(s) &= CE + \frac{1}{s(R+Ls)}E\\
I(s) &= CE + \left( \frac{1}{R}\frac{1}{s} – \frac{L}{R}\frac{1}{Ls+R} \right)E
\end{align}
逆ラプラス変換すると
\begin{align}
i(t) &= CE\delta(t) + \left( \frac{1}{R} – \frac{1}{R}e^{-\frac{R}{L}} \right)E\\
i(t) &= CE\delta(t) + \frac{E}{R}\left(1 – e^{-\frac{R}{L}} \right)
\end{align}
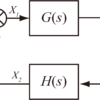
伝達関数\(G(s)\)の求め方
例題1の電源を外した回路は以下のようにも表せる.

この回路の入力を\(e_i(t)\),出力を\(e_o(t)\)とするとキルヒホッフの第二法則から
\begin{align}
e_i(t) &= Ri(t) + L\frac{d}{dt}i(t) + \frac{1}{C}\int_0^t i(t’) dt’\\
e_o(t) &= \frac{1}{C}\int_0^t i(t’) dt’
\end{align}
ラプラス変換すると
\begin{align}
E_i(s) &= RI(s) + LsI(s) + \frac{1}{Cs}I(s)\\
E_o(s) &= \frac{1}{Cs}I(s)
\end{align}
伝達関数\(G(s)=\frac{E_o(s)}{E_i(s)}\)は
\begin{align}
G(s) &= \frac{1}{Cs}I(s) \times \frac{1}{(R + Ls + \frac{1}{Cs})I(s)}\\
G(s) &= \frac{1}{Cs(R + Ls + \frac{1}{Cs})}\\
G(s) &= \frac{1}{LCs^2 + RCs + 1}
\end{align}
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p72-


ディスカッション
コメント一覧
まだ、コメントがありません