生物工学演習D -第5回- ボード線図 システムの入出力特性の解析
今回の目標
□ボード線図の意味を理解する
□伝達関数からボード線図を書く方法を理解する
周波数応答(Frequency response)
システムにサイン波入力を加えた時の定常応答を周波数応答と呼ぶ.周波数応答解析では様々な周波数の入力をシステム(電気回路など)に入れ,その応答を調べることでシステムを理解する.その結果として得られるのが次に紹介するボード線図である.
周波数応答解析の利点はシステムの数式がわからない未知のシステムに対しても実験的に調べることができる点.
ボード線図とは
ボード線図(Bode Plot)は,システム制御工学において一般的に使用されるグラフィカルな表現方法で,線形時間不変システム(Linear Time-Invariant System,LTIシステム)の周波数応答を示す.ボード線図は,システムの安定性,周波数特性,フィルタ設計,制御システムの性能評価などに役立つ.
ボード線図は,2つの部分から構成される.
chatGPT
- ゲイン線図(Magnitude plot):ゲイン線図は、システムの周波数応答の絶対値(またはゲイン)をデシベル(dB)単位でプロットしたもの。横軸は対数周波数(通常はディケード単位)で,縦軸はシステムのゲイン(dB).ゲイン線図を使って,システムが特定の周波数でどれだけのゲインを持っているかを把握することができる.
- 位相線図(Phase plot):位相線図は,システムの周波数応答の位相角をプロットしたものである.横軸は対数周波数(通常はディケード単位)で,縦軸は位相角(度単位).位相線図を使って,システムが特定の周波数でどの程度の位相遅れや進みを持っているかを把握することができる.
ボード線図を伝達関数\(G(s)\)から書く際には\(s = j\omega\)を代入します.
最初になぜそのようなことをするのか確認します.
三角関数入力に対するシステムの定常応答
安定で線形,時不変なシステムに対して信号\(u(t) = \sin(\omega t)\)を入力すると,その出力は同じ周波数で振幅と位相が変化した信号 \(y(t) = k_\omega\sin(\omega t + \theta_\omega)\)になる.
ポイント:システムが安定→システムの極\(s_i\)の実部が負
例
例えば線形時不変システム\(G(s)\)が一次の極をもつとき,\(u(t) = \sin(\omega t)\)を入力するとその出力\(Y(s)\)は
\begin{align}
Y(s) &= G(s)U(s)\\
&= G(s)\frac{\omega}{s^2+\omega^2}\\
&= \frac{a}{s-j\omega} + \frac{\bar{a}}{s+j\omega} + \frac{b_1}{s-s_1} + \frac{b_2}{s-s_2}+\dots + \frac{b_n}{s-s_n}
\end{align}
これを逆ラプラス変換すると
\begin{align}
y(t) &= ae^{j\omega t} + \bar{a}e^{-j\omega t} + b_1e^{s_1 t} + b_2e^{s_2 t}+\dots + b_ne^{s_n t}
\end{align}
この時システムの極\(s_i\)の実部が負より,\(t\rightarrow \infty\)における定常応答を考えると第一項と第二項しか残らない.
このとき各係数\(a,\bar{a}\)はそれぞれ,ヘビサイドのカバーアップ法から
\begin{align}
a &= \lim_{s \rightarrow j\omega} G(s)\frac{\omega}{s^2+\omega^2} \times (s-j\omega)\\
&= \lim_{s \rightarrow j\omega} G(s)\frac{\omega}{s+j\omega}\\
&= G(j\omega)\frac{\omega}{2j\omega}\\
&=\frac{G(j\omega)}{2j}
\end{align}
\begin{align}
\bar{a} &= \lim_{s \rightarrow -j\omega} G(s)\frac{\omega}{s^2+\omega^2} \times (s+j\omega)\\
&= \lim_{s \rightarrow -j\omega} G(s)\frac{\omega}{s-j\omega}\\
&= G(-j\omega)\frac{\omega}{-2j\omega}\\
&=\frac{G(-j\omega)}{-2j}
\end{align}
ここで\(G(j\omega)\)は複素数なので\(G(j\omega) = |G(j\omega)|e^{j\phi}\)と書ける.
ただし,\(\phi=\arctan(\frac{\text{imaginary part of } G(j\omega)}{\text{real part of } G(j\omega)})\)
(ピンとこない方は複素平面を思い出してほしい.)
同様に\(G(-j\omega) = |G(j\omega)|e^{-j\phi}\)と書ける.
よって
\begin{align}
a &= \frac{|G(j\omega)|e^{j\phi}}{2j}\\
\bar{a} &= -\frac{|G(j\omega)|e^{-j\phi}}{2j}
\end{align}
つまり,定常応答\(y(t)\)は
\begin{align}
y(t) &= \frac{|G(j\omega)|e^{j\phi}}{2j}e^{j\omega t} – \frac{|G(j\omega)|e^{-j\phi}}{2j}e^{-j\omega t} \\
&= |G(j\omega)|\frac{e^{j(\omega t +\phi)} – e^{-j(\omega t + \phi)}}{2j} \\
&= |G(j\omega)|\sin(\omega t +\phi)
\end{align}
伝達関数\(G(s)\)に周波数\(\omega\)のsin波を入力したときの定常応答は,伝達関数に\(s=j\omega\)を代入したときの絶対値\(|G(j\omega)|\)倍振幅が変化し,\(\phi\)分位相が進んだ波形になる.
以下補足—————–
線形なシステム:微分方程式モデルが係数×入出力とその微分項の和だけで表現される
時不変なシステム:時間によって微分方程式の係数が変化しない
上記性質を持つとき,重ね合わせの原理が成り立つ
\begin{align}
G(s)\times (aX_1(s) + bX_2(s)) = aG(s)X_1(s) + bG(s)X_2(s)
\end{align}
————————
現実の信号の多くは三角関数の線形和で表現できる
フーリエ級数展開により周期関数\(u(t)\)は次のようにsinとcosの和で書ける.
\begin{align}
u(t) = \frac{a_0}{2} + \sum_{k=1}^{\infty}(a_k \cos \omega_0kt + b_k \sin \omega_0kt)
\end{align}
つまり,角周波数\(\omega_0k\)に対する\(|G(j\omega_0k)|\)と\(\angle G(j\omega_0k)\)がわかれば\(y(t)\)は
\begin{align}
y(t) &= |G(0)|\frac{a_0}{2} \\
&+ \sum_{k=1}^{\infty}\{a_k|G(j\omega_0k)| \cos (\omega_0kt + \angle G(j\omega_0k)) \\
&+ b_k|G(j\omega_0k)| \sin (\omega_0kt + \angle G(j\omega_0k))\}
\end{align}
とそれぞれ別々に伝達関数に通したものの和で書ける.
ボード線図の書き方(手計算)
基本の方針は以下の通り
ゲイン線図
横軸を角周波数(対数),縦軸を\(20\log_{10}|G(j\omega)|\)としてプロット.
\(20\log_{10}|G(j\omega)|\)について\(\omega\)が十分に小さいとき,大きいとき等を考えて折れ線近似
位相線図
横軸を角周波数(対数),縦軸を\(\angle G(j\omega) = \arctan(\frac{\text{imaginary part of } G(j\omega)}{\text{real part of } G(j\omega)})\)としてプロット.
\(\angle G(j\omega) \)について\(\omega\)が十分に小さいとき,大きいとき等を考えて折れ線近似する.
例題1
\begin{align}
G(s) = K, (K>1)
\end{align}
ゲイン線図は
\begin{align}
20\log_{10}|G(j\omega)| = 20\log_{10}K, (K>1)
\end{align}
で角周波数\(\omega\)によらず一定.
位相線図は
\begin{align}
\angle G(j\omega) &= \arctan(\frac{\text{imaginary part of } G(j\omega)}{\text{real part of } G(j\omega)})\\
&= \arctan(0/K)\\
&= 0 \text{ [deg]}
\end{align}
で常に位相差0
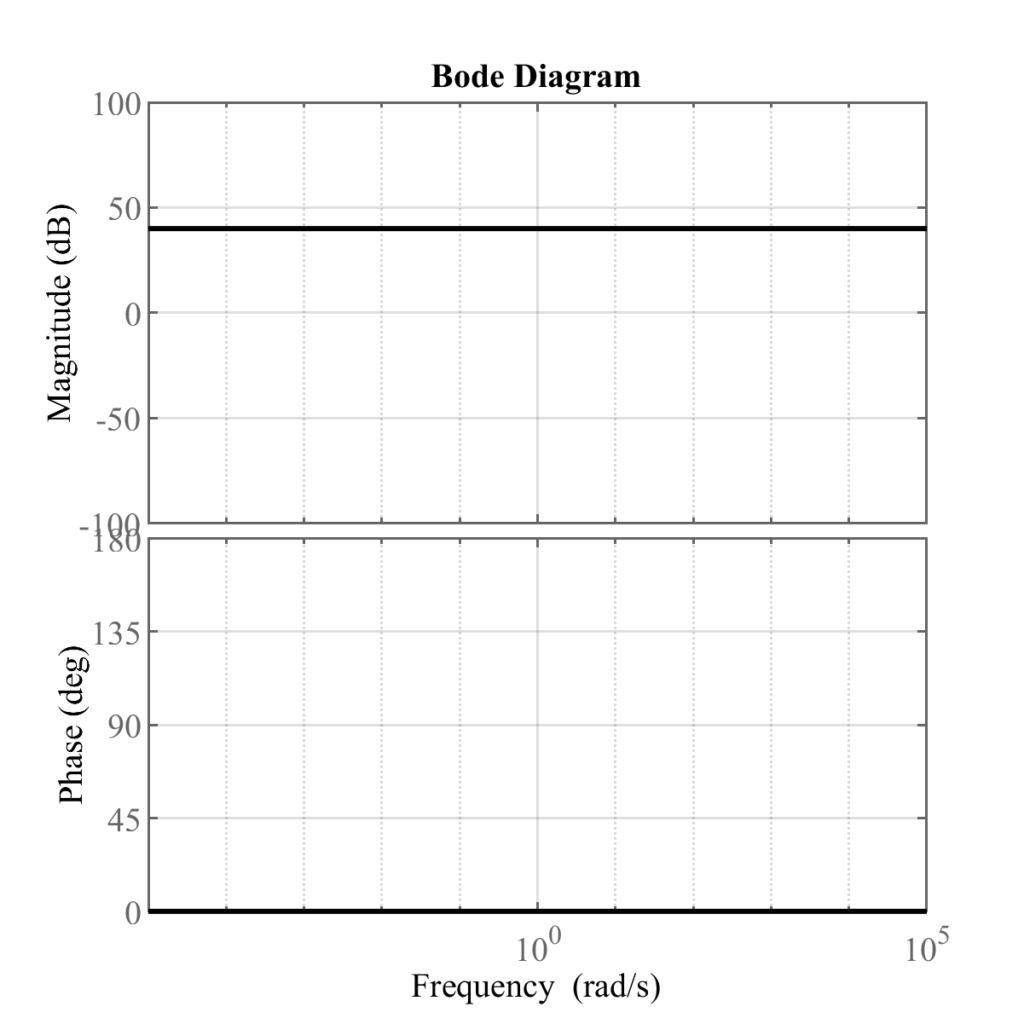
例題2
\begin{align}
G(s) = s
\end{align}
ゲイン線図は
\begin{align}
20\log_{10}|G(j\omega)| &= 20\log_{10}\sqrt{j\omega\times(-j\omega)}\\
&= 20\log_{10}\sqrt{\omega^2)}\\
&= 20\log_{10}\omega
\end{align}
で角周波数\(\omega\)が10増えるごとに\(20\log_{10}|G(j\omega)|\)は20増える(傾き20).
また,\(\omega = 1\)のとき縦軸が0の点を通る.
位相線図は
\begin{align}
\angle G(j\omega) &= \arctan(\frac{\text{imaginary part of } G(j\omega)}{\text{real part of } G(j\omega)})\\
&= \arctan(\omega/0)\\
&= \arctan(\infty) = 90 \text{ [deg]}
\end{align}
で常に位相差90度
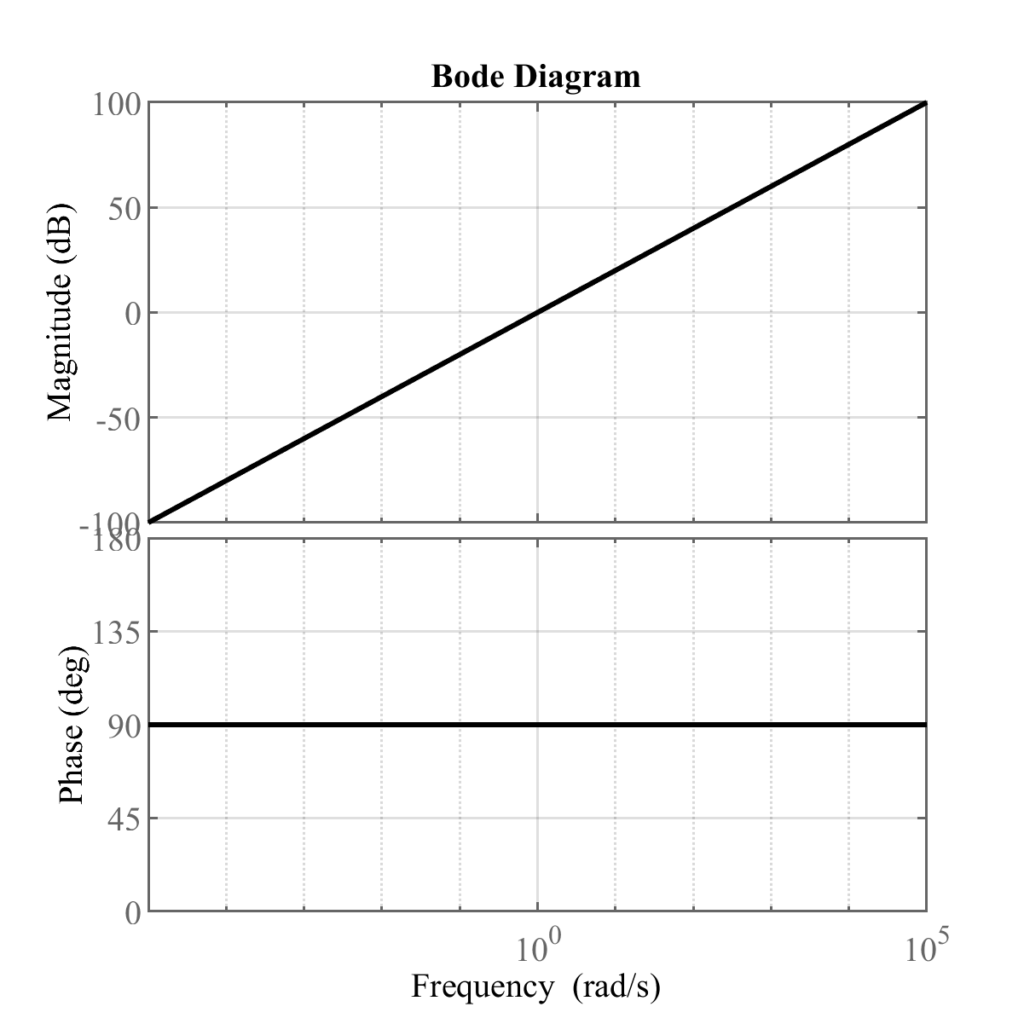
例題3
\begin{align}
G(s) = Ts+1
\end{align}
ゲイン線図は
\begin{align}
20\log_{10}|G(j\omega)| &= 20\log_{10}\sqrt{(Tj\omega+1)\times(-Tj\omega+1)}\\
&= 20\log_{10}\sqrt{1+(T\omega)^2}
\end{align}
で
(1)\(T\omega\)が1に比べて十分小さい(\(\omega \simeq 0\))とき\((T\omega)^2\)は無視することができて,
\begin{align}
20\log_{10}|G(j\omega)|
&= 20\log_{10}\sqrt{1} = 0
\end{align}
(2)\(T\omega\)が1のとき
\begin{align}
20\log_{10}|G(j\omega)|
&= 20\log_{10}\sqrt{2}\\
&= 20 \times 0.1505 = 3.010
\end{align}
(3)\(T\omega\)が1に比べて十分大きい(\(\omega \simeq \infty\))とき1は無視することができて,
\begin{align}
20\log_{10}|G(j\omega)|
&= 20\log_{10}\sqrt{(T\omega)^2}\\
&= 20\log_{10}(T\omega)
\end{align}
\(\omega\)が10増えるごとに\(20\log_{10}|G(j\omega)|\)は20増える(傾き20).
また,\(\omega =1/T\)のとき縦軸が0の点を通る.
位相線図も同様に(1)-(3)の条件を考える.
まず
\begin{align}
\angle G(j\omega) &= \arctan(\frac{\text{imaginary part of } G(j\omega)}{\text{real part of } G(j\omega)})\\
&= \arctan(T\omega/1)\\
&= \arctan(T\omega)
\end{align}
(1)\(\omega \simeq 0\)のとき
\begin{align}
\angle G(j\omega) &= \arctan(T\omega)\\
&\simeq \arctan(0) = 0\text{ [deg]}
\end{align}
(2)\(T\omega = 1\)のとき
\begin{align}
\angle G(j\omega) &= \arctan(T\omega)\\
&= \arctan(1) = 45\text{ [deg]}
\end{align}
(3)\(\omega \simeq \infty\)のとき
\begin{align}
\angle G(j\omega) &= \arctan(T\omega)\\
&\simeq \arctan(\infty) = 90\text{ [deg]}
\end{align}
たとえば\(T=100\)のときのボード線図は以下のようになる.\(1/T=10^{-2}\)を基準にゲイン特性が大きく変化していることが確認できる.
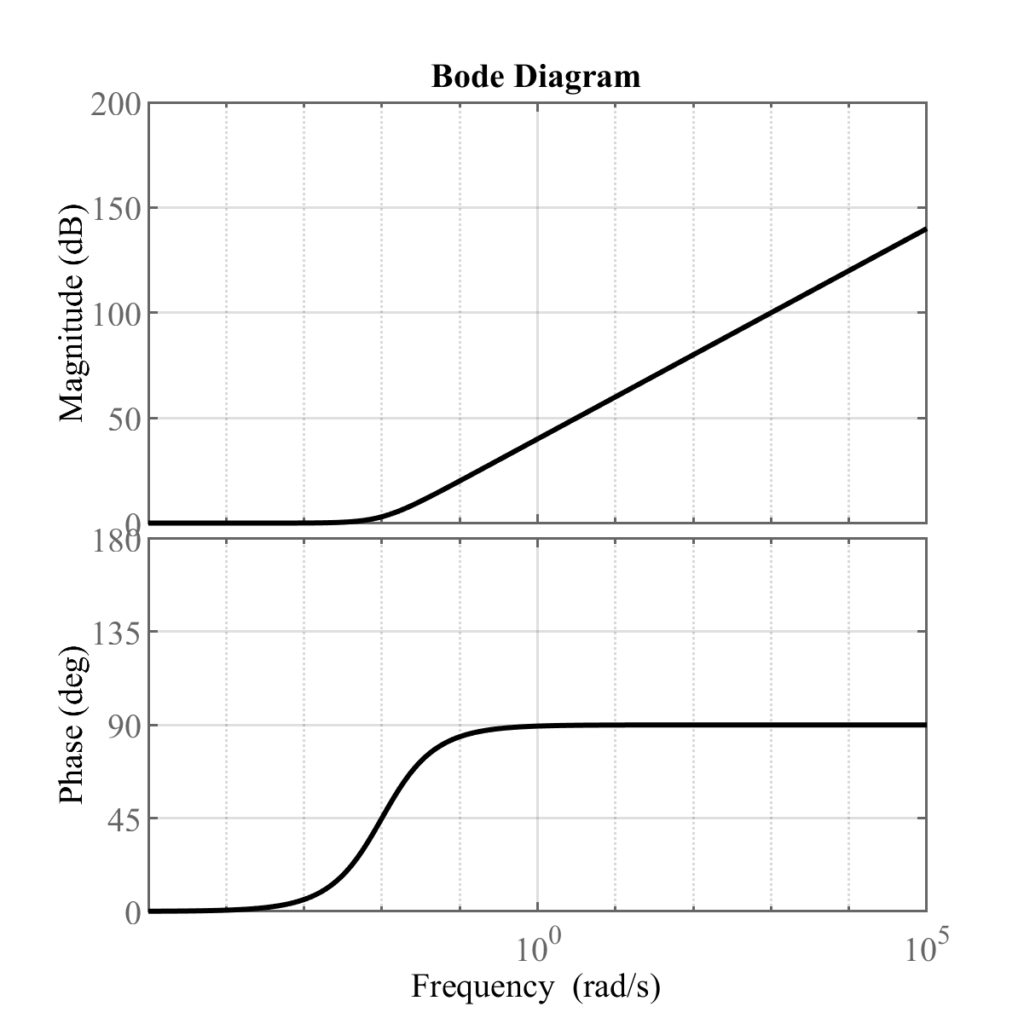
例題4
\begin{align}
G(s) = (100s+1)(0.01s+1)
\end{align}
\begin{align}
G(s) = (100s+1) \times (0.01s+1) = G_1(s) \times G_2(s)
\end{align}
と考えると,\(G_1(s)\)は例題3の\(T=100\),\(G_2(s)\)は例題3の\(T=0.01\)の場合に対応することがわかる.
ゲイン線図はこのとき
\begin{align}
20\log_{10}|G(j\omega)| &= 20\log_{10}|G_1(j\omega)G_2(j\omega)|\\
&= 20\log_{10}|G_1(j\omega)||G_2(j\omega)|\\
&= 20\log_{10}|G_1(j\omega)| + 20\log_{10}|G_2(j\omega)|
\end{align}
と足し算で表せる(あえてlogをとってプロットする理由).
よってゲイン線図は\(G_1\)と\(G_2\)のゲイン線図の和となる
\begin{align}
20\log_{10}|G(j\omega)| &= 20\log_{10}(100\omega) + 20\log_{10}(0.01\omega)
\end{align}
位相線図も同様に\(\angle G_1(j\omega)\)と\(\angle G_2(j\omega)\)の位相線図の和として表される(複素平面で考えてみるとわかりやすい).
\(G_1\)のボード線図は以下
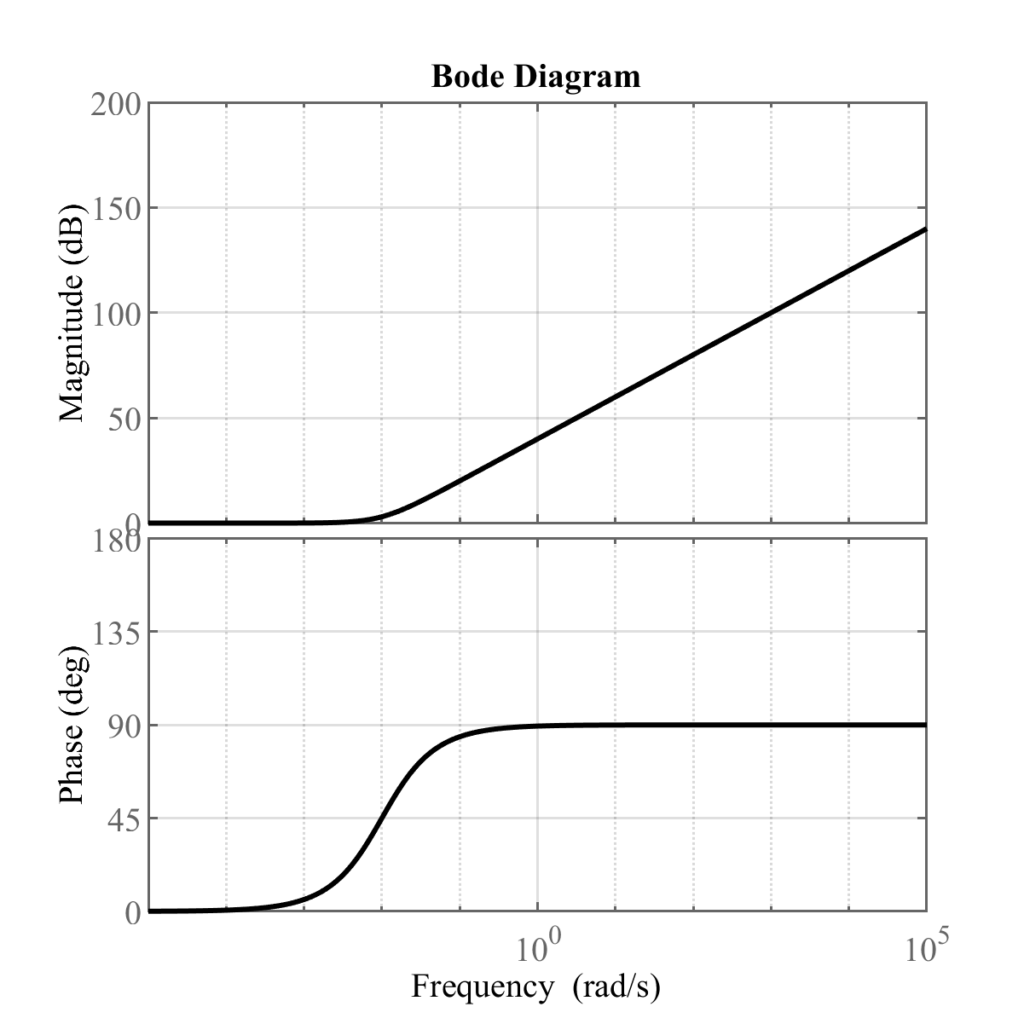
\(G_2\)のボード線図は以下
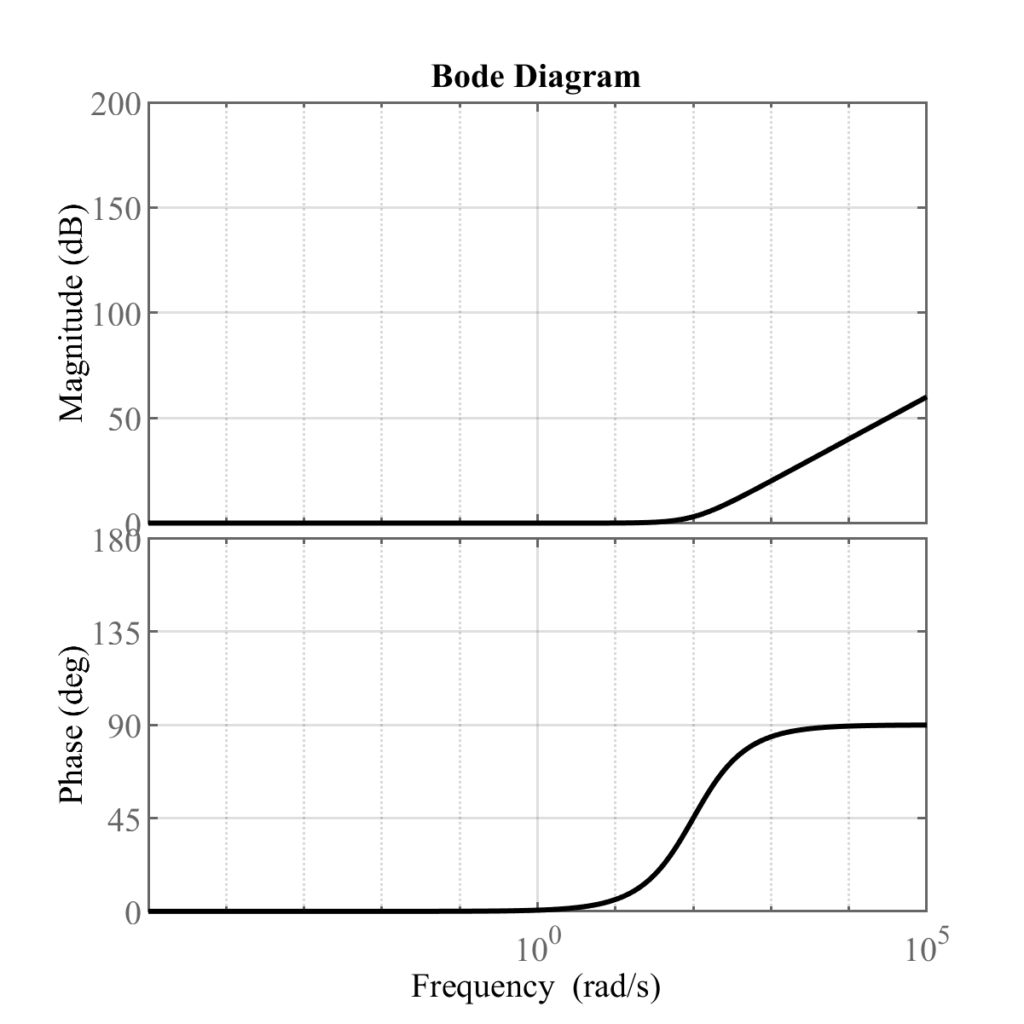
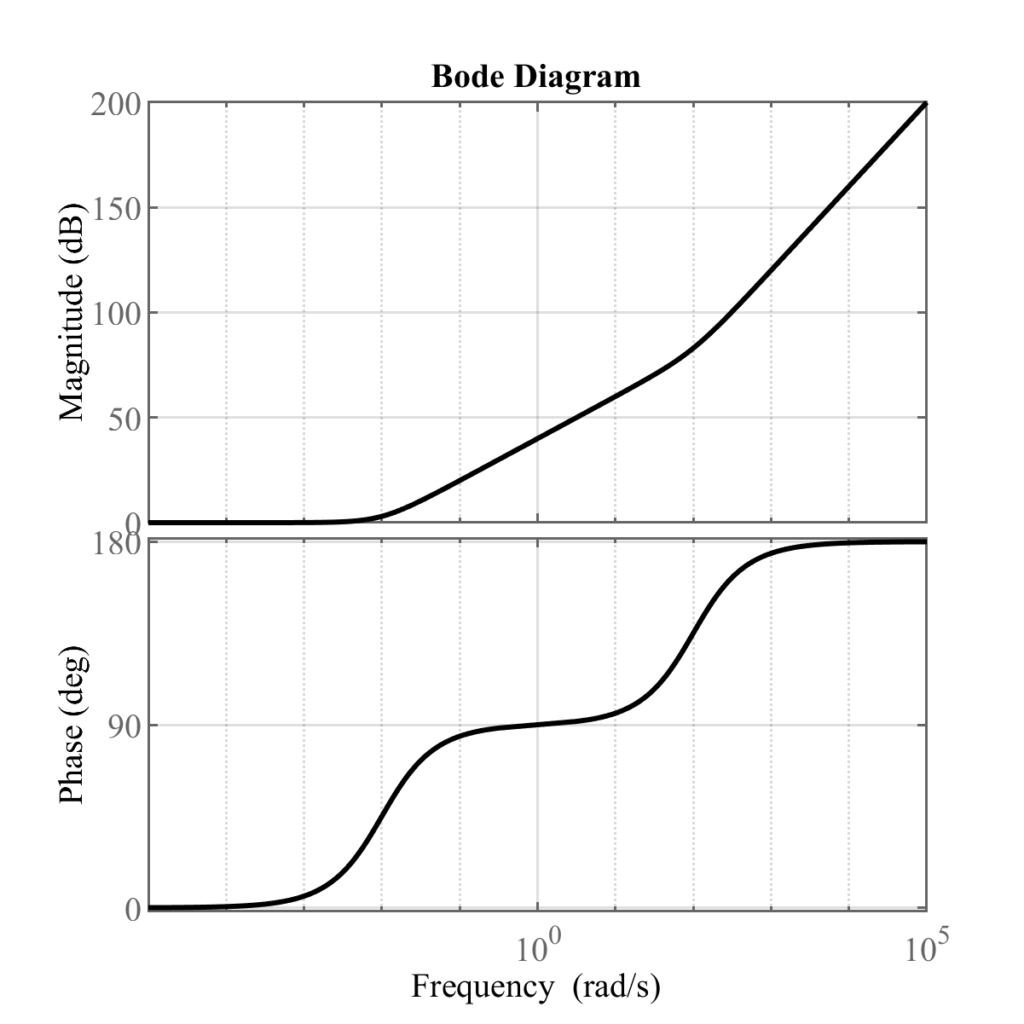
よって解答のボード線図は以下のようになる
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p398-



ディスカッション
コメント一覧
まだ、コメントがありません