生物工学演習E -第3回- 位相を複素数で表現,複素フーリエ級数展開
今回の目的
複素フーリエ級数展開の計算を身に着ける
\(\sin,\cos\)で内積をとっていたのは位相を表すため
前回,連続周期信号\(x(\cdot)\)を\(\sin,\cos\)からなる直交基底関数を使って分解するフーリエ級数展開を学んだ.
それは以下のように表される.
\begin{align}
x(t) = a_0\times 1 + \sum_{k=1}^{\infty}\{a_k \cos(k\omega t) + b_k \sin(k\omega t)\}
\end{align}
ここで\(\omega = \frac{2\pi}{T}\)である.
\begin{align}
a_0&=\frac{1}{\|1\|^2}\langle x(t), 1 \rangle \\
&= \frac{1}{T}\int_{-T/2}^{T/2} x(t) \times 1 dt\\
\end{align}
\begin{align}
a_k&=\frac{1}{\|\cos k \omega t\|^2}\langle x(t), \cos k \omega t \rangle \\
&= \frac{2}{T}\int_{-T/2}^{T/2} x(t) \cos k \omega t dt\\
\end{align}
\begin{align}
b_k&=\frac{1}{\|\sin k \omega t\|^2}\langle x(t), \sin k \omega t \rangle \\
&= \frac{2}{T}\int_{-T/2}^{T/2} x(t) \sin k \omega t dt\\
\end{align}
ところで,同じ周波数なのに\(\sin,\cos\)という2つの波が必要なのはなぜだろうか?
実は同じ周波数でも\(\sin k \omega t\)と \(\cos k \omega t\)の和をとることによってその周波数の波の大きさだけでなく位相を表しているのである.
このことは\(\sin,\cos\)の合成の公式を考えてもらうとわかりやすい.
\begin{align}
a_k \cos k \omega t + b_k \sin k \omega t &= \sqrt{a_k^2 + b_k^2}\left( \frac{a_k}{\sqrt{a_k^2 + b_k^2}} \cos k \omega t + \frac{b_k}{\sqrt{a_k^2 + b_k^2}} \sin k \omega t \right )\\
&= \sqrt{a_k^2 + b_k^2}\left( \sin \alpha \cos k \omega t + \cos \alpha \sin k \omega t \right )\\
&= \sqrt{a_k^2 + b_k^2}\sin (k \omega t + \alpha)
\end{align}
このように\(\sin\)と\(\cos\)という二つの波によってある周波数の波の大きさ\(\sqrt{a_k^2 + b_k^2}\)と位相\(\alpha = \arccos \frac{a_k}{\sqrt{a_k^2 + b_k^2}}\)を表現しているのである.
つまり,\(a_k, b_k\)はある周波数の波の振幅と位相の間接的な表現となっている.
もっとうまく直接的に振幅と位相の両方を扱えないだろうか…
そこで出てくるのが複素数およびその極形式であり,複素フーリエ級数展開である.
複素数と複素平面上の位相と振幅
複素数は\(c=a+jb\)と書ける.複素平面上で考えたとき,複素数\(c\)の座標は\((a,b)\)で表すことができるが極形式で考えると振幅\(r\)と位相\(\alpha\)を使って\((r,\alpha)\)で表すこともできる.
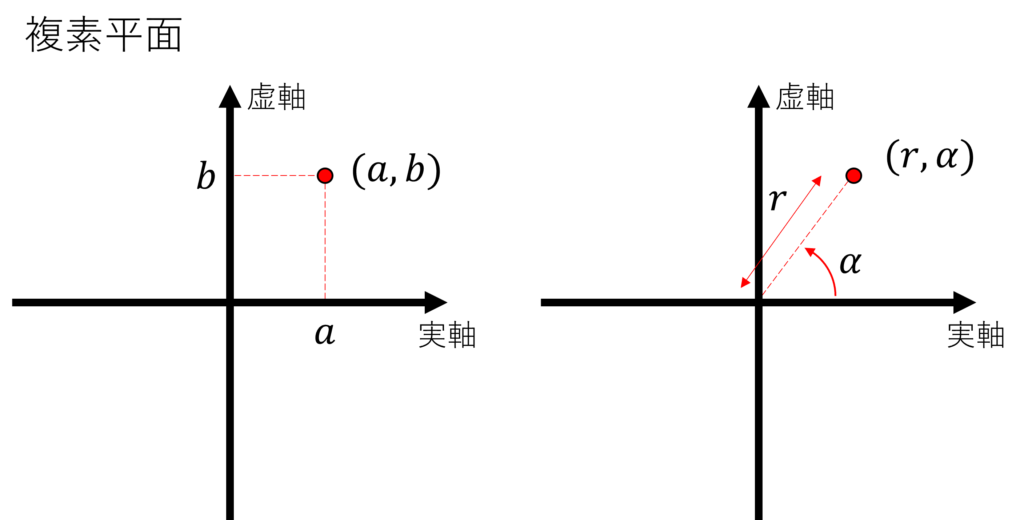
このとき複素数は\(c=a+jb=r\cos\alpha + jr\sin \alpha \)である.
ここでオイラーの公式\(e^{j \alpha} = \cos\alpha + j\sin \alpha \)を思い出すと,複素数\(c\)は
\begin{align}
c = r e^{j \alpha}
\end{align}
と表せる.
また複素数\(c_2\)に\(c_1\)をかけることは複素平面において,元の複素数の振幅を\(r_1\)倍し偏角を\(\alpha_1\)進めることに対応する.
\begin{align}
c_1\times c_2 = r_1 e^{j \alpha_1}r_2 e^{j \alpha_2} = r_1r_2 e^{j (\alpha_1 + \alpha_2)}
\end{align}
つまり,複素数の極形式は掛け算によって元の複素数の振幅と位相を自然な形で変化させることができる.
連続周期信号\(x(\cdot)\)を波の和で近似する際に,\(\sin,\cos\)関数系を基底関数として,実数の係数\(a_k,b_k\)の組み合わせによって間接的に振幅と位相を表現する代わりに,
複素指数関数\(e^{jk\omega t}\)からなる複素関数系(これも波を表現している)を基底関数として,極形式の複素係数をかけることにより,直接的に位相と振幅を表現したのが複素フーリエ級数展開である.
複素フーリエ級数展開
複素フーリエ級数展開では連続周期信号\(x(\cdot)\)を波を表す複素指数関数とその係数である複素フーリエ係数\(X_k\)を用いて以下のように展開する.
\begin{align}
x(t) \sim \sum_{k=-\infty}^{\infty}X_ke^{jk\omega t}
\end{align}
ここで\(\omega = \frac{2\pi}{T}\)である.
このとき複素フーリエ係数\(X_k\)は以下の内積の結果複素数として得られる.
\begin{align}
X_k &=\frac{1}{\|e^{jk\omega t}\|^2}\langle x(t), e^{jk\omega t} \rangle \\
&= \frac{1}{T}\int_{-T/2}^{T/2} x(t) \times (e^{jk\omega t})^* dt\\
&= \frac{1}{T}\int_{-T/2}^{T/2} x(t) \times e^{-jk\omega t} dt
\end{align}
ここでアスタリスク(*)は複素共役を表す.
複素関数の内積を定義する場合,以下のように定義される.
\begin{align}
\langle x, y \rangle
&= \int_{-T/2}^{T/2} x(t) \times y^*(t) dt
\end{align}
上記のように内積の対象となる2つの関数の内どちらか一方の複素共役をとることは複素数の絶対値の計算方法を思い出すと感覚的に理解できる.
複素数\(c=a+jb\)の絶対値\(|a|\)は以下のように
\begin{align}
|c|
&= \sqrt{c\times c^*}\\
&= \sqrt{(a+jb)(a-jb)}\\
&= \sqrt{a^2+b^2}
\end{align}
\begin{align}
||x|| &=
\sqrt{\langle x, x \rangle}\\
&= \sqrt{\int_{-T/2}^{T/2} x(t) \times x^*(t) dt}
\end{align}
実フーリエ級数展開では\(\sin,\cos\)関数系が基底関数だったが,複素フーリエ級数展開では\(\{ \dots, e^{-j\omega t}, e^{0\times j\omega t}, e^{j\omega t}, \dots, e^{jk\omega t}, \dots \}\)のように複素指数関数系を基底関数とする.
この複素指数関数系においても,直交性があり内積計算によってフーリエ係数を求めることができる(演習問題).
・複素フーリエ係数は\(X_k = X_{-k}^*\)の関係を持つ.
・\(e^{jk\omega t}\)と\(e^{-jk\omega t}\)の組み合わせで角周波数\(k\omega\)の波を表す.


ディスカッション
コメント一覧
まだ、コメントがありません