生物工学演習E -第10回- 離散システムのz変換による解析
今回の概要
z変換で離散システムを解析する手法を理解する.
z変換の定義(復習)
信号\(x(t)\)のz変換は以下のように定義される.
\begin{align}
X(z) = \sum_{n=0}^\infty x_n z^{-n}
\end{align}
ここで\(z =e^{\tilde{s}} = e^{\tilde{\sigma} + j \tilde{\omega}}\)である.
z変換による離散システムの解析
連続線形時不変システムでは微分方程式をラプラス変換し,その入出力関係を伝達関数で表した.
さらに伝達関数からシステムの極を求め,インパルス入力に対してそのシステムの安定性を求めた.
ラプラス変換の離散版であるz変換は,離散システムに対して同様の計算を行うことができる.以下ではそのことを確認していく.
微分方程式の差分方程式化
例として以下の回路を考えていく.
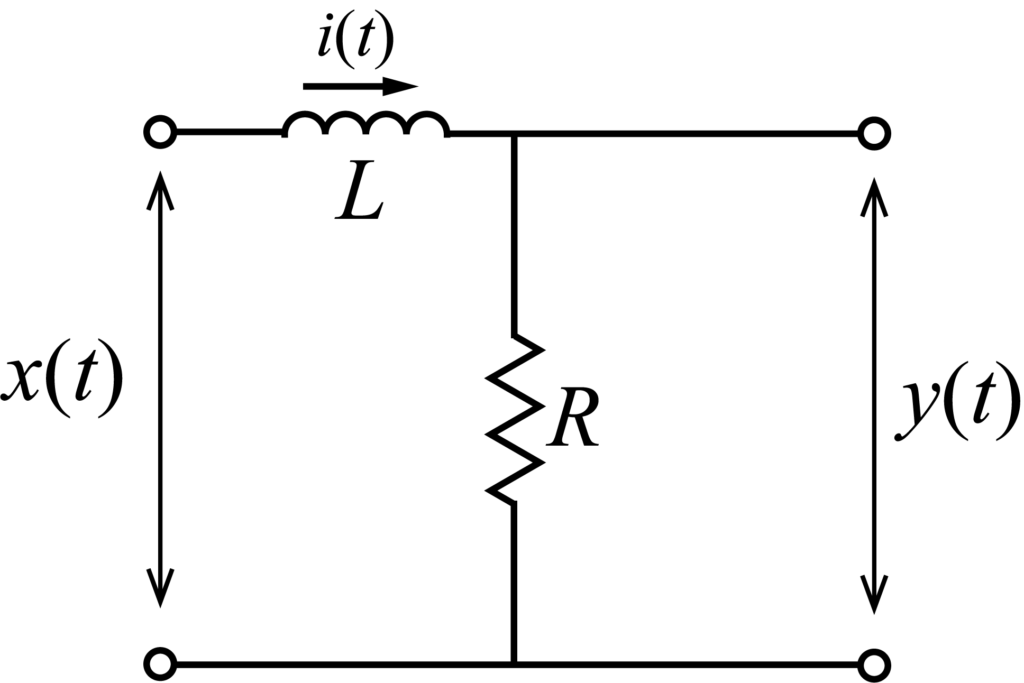
このシステムの微分方程式は次のように立式される.
\begin{align}
x(t) &= L\frac{di}{dt}(t) + Ri(t)\\
y(t) &= Ri(t)
\end{align}
\(i(t)\)を消して一つの式にすると
\begin{align}
x(t) &= \frac{L}{R}\frac{dy}{dt}(t) + y(t)
\end{align}
この式を後退差分で差分方程式に変換すると
\begin{align}
x_{n} &= \frac{L}{R}\frac{y_n-y_{n-1}}{\Delta} + y_n\\
x_{n} &= (1+\frac{L}{R\Delta})y_n – \frac{L}{R\Delta}y_{n-1}\\
y_{n} &= \frac{1}{(1+\frac{L}{R\Delta})}x_n – \frac{\frac{L}{R\Delta}}{(1+\frac{L}{R\Delta})}y_{n-1}
\end{align}
離散システムの種類
離散システムの入出力関係を一般化すると以下のようにかける.
\begin{align}
y_{n} &= \sum_{l=1}^{L} a_ly_{n-l} + \sum_{m=0}^{M}b_m x_{n-m}
\end{align}
離散システムは,時刻\(n\)の出力がその後の時刻に影響を与えないかどうか,つまり全ての\(l\)について\(a_l=0\)かどうかで大きく二つに分けられる.
有限インパルス応答(Finite impulse response, FIR)システム
全ての\(l\)について\(a_l=0\)となるような離散システムは非再帰型と呼ばれ以下の式で表される.
\begin{align}
y_{n} &= \sum_{m=0}^{M}b_m x_{n-m}
\end{align}
後ほど説明するがこのタイプのシステムにインパルス入力を入れるとその応答は有限時間で0になる.
無限インパルス応答(Infinite impulse response, IIR)システム
\(l\)について一つでも\(a_l\neq 0\)となるような離散システムは再帰型と呼ばれ以下の式で表される.
\begin{align}
y_{n} &= \sum_{l=1}^{L} a_ly_{n-l} + \sum_{m=0}^{M}b_m x_{n-m}
\end{align}
離散システムのz変換と伝達関数
\begin{align}
y_{n} &= \sum_{l=1}^{L} a_l y_{n-l} + \sum_{m=0}^{M}b_m x_{n-m}
\end{align}
をz変換すると
\begin{align}
Y(z) &= \sum_{l=1}^{L} a_l z^{-l}Y(z) + \sum_{m=0}^{M}b_m z^{-m}X(z)\\
(1-\sum_{l=1}^{L} a_l z^{-l})Y(z) &= \sum_{m=0}^{M}b_m z^{-m}X(z)
\end{align}
離散システムの伝達関数を\(H(z)=\frac{Y(z)}{X(z)}\)とすると
\begin{align}
H(z) = \frac{Y(z)}{X(z)} &= \frac{\sum_{m=0}^{M}b_m z^{-m}}{(1-\sum_{l=1}^{L} a_l z^{-l})}
\end{align}
インパルス入力に対する応答
連続システムと同様離散システムにおいてもインパルス入力に対する応答はシステムの特性を表す.
インパルス入力
\begin{align}
\delta_n = \left\lbrace \begin{array}{cl}1 & \text{when $n = 0$} \\ 0 & \text{otherwise}\end{array}\right.
\end{align}
に対する以下のシステムの応答は次のようになる
\begin{align}
y_{n} &= \sum_{l=1}^{L} a_ny_{n-l} + \sum_{m=0}^{M}b_m x_{n-m}
\end{align}
\begin{align}
y_0 &= b_0\\
y_1 &= a_1y_0 + b_1\\
y_2 &= a_1y_1 + a_2y_0 + b_2\\
\vdots \\
y_n &= a_1y_n + a_2y_{n-1} + \dots + a_ny_0 + b_n\\
\end{align}
システムの安定性
伝達関数の極からシステムの安定性がわかる.
伝達関数の極は\(H(z)=\infty\)を満たす\(z\)の値.
極を\(z_p\)とすると\(|z_p|<1\)が全ての極について成り立つならばそのシステムは安定である.
例
\begin{align}
H(z) &= \frac{1}{(1-az^{-1})}
\end{align}
というシステムの極は\(z_p=a\)でありそのインパルス応答は\(y_n=a^n\)となる.
このとき極の実部\(Re(z_p)\)の正負および,その絶対値が1を超えるかどうかによってシステムのふるまいが変化する.
この微分方程式を後退差分で離散化すると
\begin{align}
x_{n} &= L\frac{i_n-i_{n-1}}{\Delta} + Ri_n\\
y_{n} &= Ri_n
\end{align}
これらをz変換すると
\begin{align}
X(z) &= L\frac{I(z)-z^{-1}I(z)}{\Delta} + RI(z)\\
Y(z) &= RI(z)
\end{align}
伝達関数\(H(z)=\frac{Y(z)}{X(z)}\)を計算すると
\begin{align}
H(z) &= \frac{RI(z)}{L\frac{I(z)-z^{-1}I(z)}{\Delta} + RI(z)}\\
&= \frac{R}{L\frac{1-z^{-1}}{\Delta} + R}\\
&= \frac{R\Delta}{L-Lz^{-1} + R\Delta}\\
&= \frac{R\Delta}{L + R\Delta -Lz^{-1}}
\end{align}


ディスカッション
コメント一覧
まだ、コメントがありません