生物工学演習D -第6回- 電気回路のボード線図
今回の目標
□フィルタ回路について理解する
□フィルタ回路を直列につないだ場合のボード線図について理解する
フィルタ回路
抵抗,コンデンサ,コイルなどの素子からなる回路はそのつなぎ方によって特定の周波数を遮断,または透過させるフィルタとなる.
例として
- ローパスフィルタ:低周波信号を透過し,高周波信号を遮断する.(例,RC回路)
- ハイパスフィルタ:高周波信号を透過させ,低周波信号を遮断
- バンドパスフィルタ:特定の周波数範囲内の信号を透過させ,その範囲外の信号を遮断
などがある.
ローパスフィルタの例(RC回路)
ローパスフィルタの例として抵抗とコンデンサからなるRC回路を考える.

キルヒホッフの第二法則からこの回路の微分方程式は以下のようになる.
\begin{align}
e_i(t) &= Ri(t) + \frac{1}{C}\int_0^t i(t’) dt’\\
e_o(t) &= \frac{1}{C}\int_0^t i(t’) dt’
\end{align}
ラプラス変換すると
\begin{align}
E_i(s) &= RI(s) + \frac{1}{Cs}I(s)\\
E_o(s) &= \frac{1}{Cs}I(s)
\end{align}
よって伝達関数\(G(s)=\frac{E_o(s)}{E_i(s)}\)は
\begin{align}
G(s) &= \frac{1}{Cs}I(s) \times \frac{1}{(R + \frac{1}{Cs})I(s)}\\
G(s) &= \frac{1}{Cs(R + \frac{1}{Cs})}\\
G(s) &= \frac{1}{RCs + 1}
\end{align}
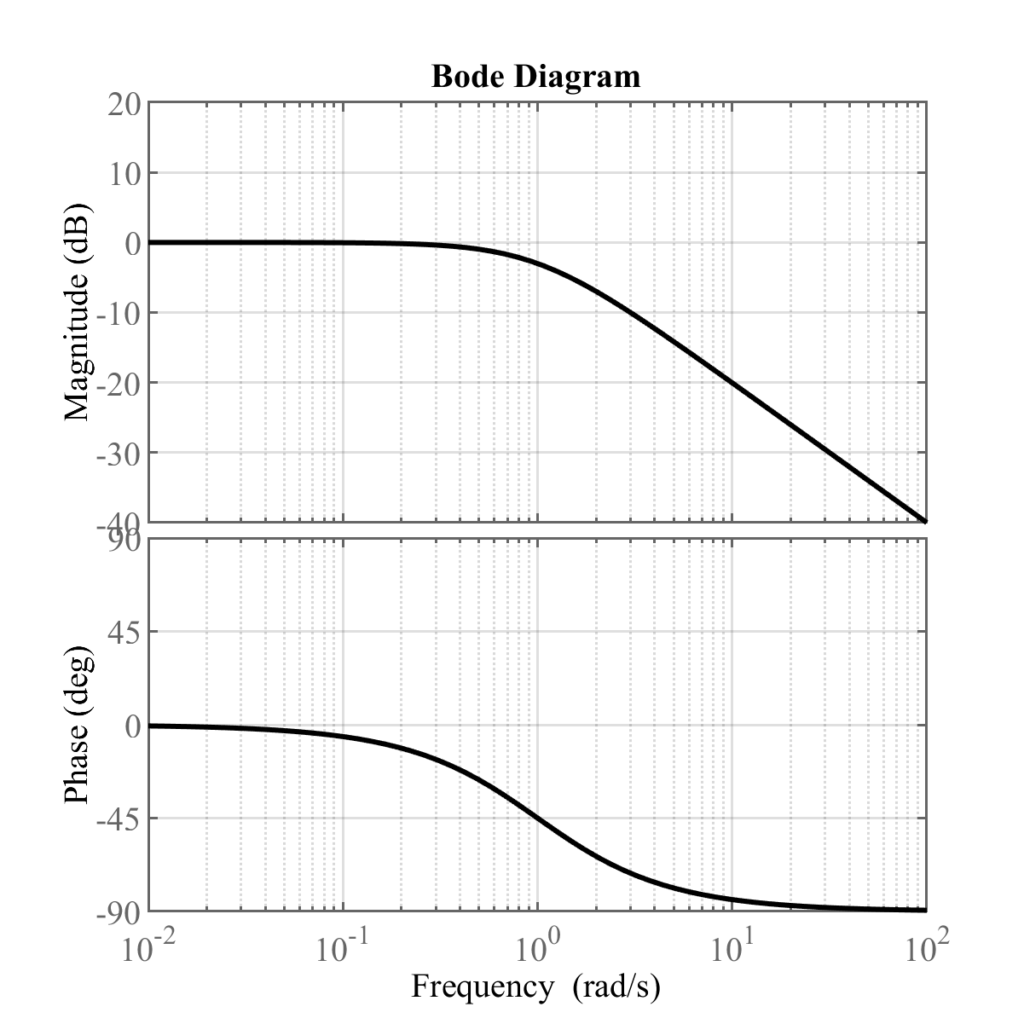
これは第5回で扱った一次遅れ系で\(T=RC\)と置いたときに対応する.
つまりボード線図は以下のようになる(R=1,C=1の場合)
ハイパスフィルタの例(RL回路)
同様にハイパスフィルタの例としてRL回路についても考える.
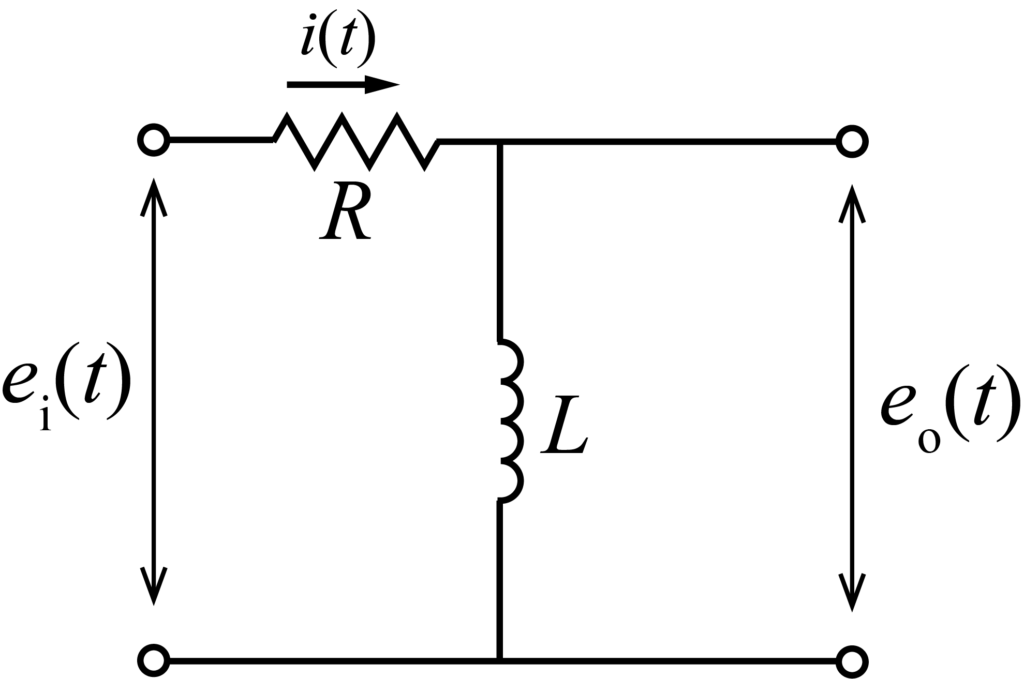
キルヒホッフの第二法則からこの回路の微分方程式は以下のようになる.
\begin{align}
e_i(t) &= Ri(t) + L\frac{d}{dt}i(t)\\
e_o(t) &= L\frac{d}{dt}i(t)
\end{align}
ラプラス変換すると
\begin{align}
E_i(s) &= RI(s) + LsI(s)\\
E_o(s) &= LsI(s)
\end{align}
よって伝達関数\(G(s)=\frac{E_o(s)}{E_i(s)}\)は
\begin{align}
G(s) &= LsI(s) \times \frac{1}{(R + Ls)I(s)}\\
G(s) &= \frac{Ls}{R + Ls}
\end{align}
\(s=j\omega\)を代入してゲインと位相を考えると,
\begin{align}
G(j\omega) &= \frac{Lj\omega}{R + Lj\omega}\\
G(j\omega) &= \frac{Lj\omega}{R^2+(L\omega)^2}(R – Lj\omega)\\
G(j\omega) &= \frac{1}{R^2+(L\omega)^2}((L\omega)^2 + jRL\omega)\\
\end{align}
\begin{align}
|G(j\omega)| &= \frac{L\omega}{\sqrt{R^2 + (L\omega)^2}}
\end{align}
\begin{align}
\angle G(j\omega) &= \arctan\left(\frac{RL\omega}{(L\omega)^2}\right)\\
\angle G(j\omega) &= \arctan\left(\frac{R}{L\omega}\right)
\end{align}
(1) \(\omega \ll \frac{R}{L}\)のとき
\begin{align}
20\log_{10}|G(j\omega)| &= 20\log_{10}\frac{L\omega}{R}
\end{align}
つまり傾き20で\(\omega = \frac{R}{L}\)のときに0を通る直線で近似できる.
\begin{align}
\angle G(j\omega) &= \arctan\left(\frac{R}{0}\right)\\
&=90 \text{[deg]}
\end{align}
位相差は90度
(2) \(\omega = \frac{R}{L}\)のとき
\begin{align}
20\log_{10}|G(j\omega)| &= 20\log_{10}\frac{1}{\sqrt{2}} \simeq -3
\end{align}
このように-3dBゲインが減少する点を折点周波数とよぶ.
\begin{align}
\angle G(j\omega) &= \arctan\left(1\right)\\
&= 45 \text{[deg]}
\end{align}
(3) \(\omega \gg \frac{R}{L}\)のとき
\begin{align}
20\log_{10}|G(j\omega)| &= 20\log_{10}1 = 0
\end{align}
\begin{align}
\angle G(j\omega) &= \arctan\left(\frac{R}{L\infty}\right)\\
&=0 \text{[deg]}
\end{align}
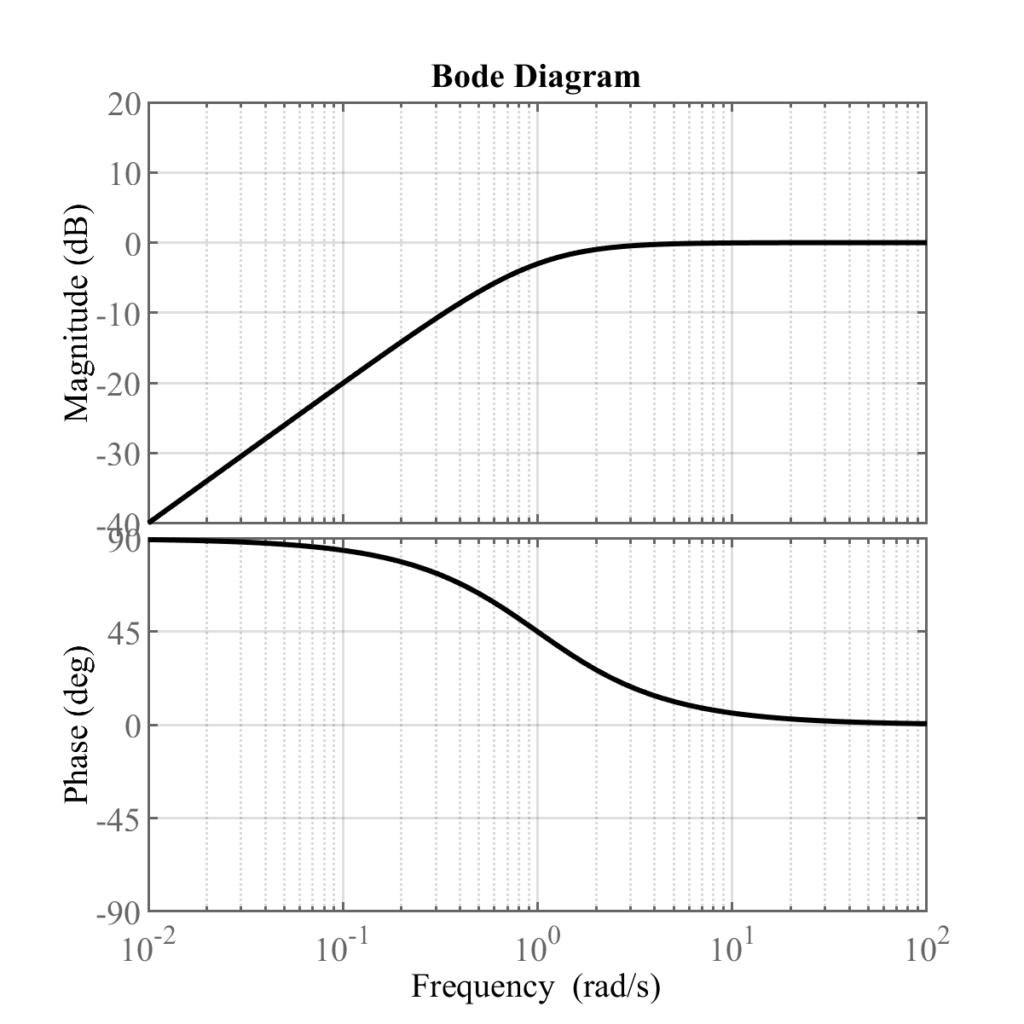
(1)-(3)からボード線図は以下のようにかける(R=1,L=1の場合)
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p398-


ディスカッション
コメント一覧
まだ、コメントがありません