生物工学演習D -第7回- 2次遅れ系 システムの極とダイナミクスの関係
今回の目標
□システムの極とダイナミクスの関係を理解する
□2次遅れ系について理解する
システムの極
\begin{align}
G(s) &= \frac{b_ms^m + b_{m-1}s^{m-1}+\dots+ b_0}{a_n s^n + a_{n-1}s^{n-1}+\dots+a_0}
\end{align}
このとき,\(m<n\)で分子と分母に共通の因子を持たないとき\(G(s)\)はn次系と呼ばれる.
n次系の分母を因数分解すると
\begin{align}
G(s) &= K\frac{(s-z_1)(s-z_2)\dots(s-z_m)}{(s-s_1)(s-s_2)\dots(s-s_n)}
\end{align}
このとき,\(s_1,s_2,\dots,s_n\)をシステムの極という.
極を調べることでシステムの安定性やふるまいがわかる.
全ての極の実部が負->安定
極の実部がすべて負の場合,インパルス応答を考えると逆ラプラス変換したときに\(e\)の肩にのる係数が負となり\(t \rightarrow \infty\)で0になる.
極の実部が一つでも正->不安定
極の実部が一つでも正の場合,その項は\(e\)の肩にのる係数が正となり\(t \rightarrow \infty\)で\(\infty\)に発散する.
2次遅れ系
2次遅れ系とは以下の微分方程式で記述されるような線形時不変システム.
\begin{align}
a\frac{d^2}{dt^2}x(t) + b\frac{d}{dt}x(t)+cx(t) = u(t)
\end{align}
これをラプラス変換すると(初期位置,速度を0とする)
\begin{align}
as^2X(s) + bsX(s)+cX(s) &= U(s)\\
(as^2 + bs+c)X(s) &= U(s)\\
G(s) &= \frac{X(s)}{U(s)}\\
&= \frac{1}{as^2 + bs+c}\\
&= \frac{\frac{1}{a}}{s^2 + \frac{b}{a}s+\frac{c}{a}}\\
\end{align}
2次遅れ系の伝達関数は係数の意味を理解しやすくするために以下のように表現される.
\begin{align}
G(s) &= \frac{K\omega_n^2}{s^2 + 2\zeta\omega_n s+\omega_n^2}
\end{align}
ただし,\(\omega_n = \sqrt{\frac{c}{a}}\),\(\zeta = \frac{b}{2\sqrt{ac}} \),\(K=\frac{1}{c}\).\(\omega_n\)は自然周波数,\(\zeta\)は減衰比と呼ばれる.
2次遅れ系の極
すこし\(G(s)\)を変形すると
\begin{align}
G(s) &= \frac{K\omega_n^2}{s^2 + 2\zeta\omega_n s+\omega_n^2}\\
&= \frac{K\omega_n^2}{(s-(-\zeta\omega_n + \omega_n \sqrt{\zeta^2-1}))(s-(-\zeta\omega_n – \omega_n \sqrt{\zeta^2-1}))}\\
&= \frac{K\omega_n^2}{(s-s_1)(s-s_2)}
\end{align}
ここで\(s_1 = -\zeta\omega_n + \omega_n \sqrt{\zeta^2-1}\),\(s_2 = -\zeta\omega_n – \omega_n \sqrt{\zeta^2-1}\).
また\(s_1, s_2\)をシステムの極という.
2次遅れ系の\(G(s)\)にインパルス応答\(u(t)=\delta(t)\)を入れた場合を考えると
\begin{align}
X(s) &= G(s)U(s)\\
&= \frac{K\omega_n^2}{(s-s_1)(s-s_2)} \times 1 \\
&= \frac{K\omega_n^2}{(s-s_1)(s-s_2)}
\end{align}
部分分数分解すると(\(s_1 \neq s_2\)のとき)
\begin{align}
X(s) &= \frac{K\omega_n^2}{(s-s_1)(s-s_2)}\\
&= \frac{K\omega_n^2}{(s_1-s_2)(s-s_1)} + \frac{K\omega_n^2}{(s_2-s_1)(s-s_2)}
\end{align}
逆ラプラス変換すると
\begin{align}
x(t) &= \frac{K\omega_n^2}{(s_1-s_2)}e^{s_1 t} + \frac{K\omega_n^2}{(s_2-s_1)}e^{s_2 t}
\end{align}
\(s_1 = -\zeta\omega_n + \omega_n \sqrt{\zeta^2-1}\),\(s_2 = -\zeta\omega_n – \omega_n \sqrt{\zeta^2-1}\)であることを思い出すと
\begin{align}
x(t) &= \frac{K\omega_n^2}{2\omega_n \sqrt{\zeta^2-1}}e^{(-\zeta\omega_n + \omega_n \sqrt{\zeta^2-1}) t} + \frac{K\omega_n^2}{-2\omega_n \sqrt{\zeta^2-1}}e^{(-\zeta\omega_n – \omega_n \sqrt{\zeta^2-1}) t}
\end{align}
つまり\(\zeta^2-1\)によってインパルス応答のふるまいは次のように変化する.ただし,\(\omega_n\)は定義より非負,\(\zeta\)も通常粘性係数\(b\)が非負のため非負の場合のみを考える.
\(\zeta^2-1=0\)つまり\(\zeta=1\)のとき臨界減衰(Critically damped)
\(\zeta=1\)のときシステムの極\(s_1,s_2\)は
\(s_1 = s_2 = -\omega_n\)となる.常に負で安定.
\(\zeta^2-1>0\)つまり\(\zeta>1\)のとき過減衰(Overdamped)
\(\zeta>1\)のときシステムの極\(s_1,s_2\)は
\(s_1 = \omega_n (\sqrt{\zeta^2-1}-\zeta)\),\(s_2 = – \omega_n (\sqrt{\zeta^2-1}+\zeta)\)となる.
このとき\(s_1,s_2\)は常に負となる.また,\(-\omega_n<s_1<0\),\(s_2<-\omega_n<0\)である点に注目すると,\(\zeta=1\)のときよりもゆっくりと目標値に近づいていくことがわかる.
\(\zeta^2-1<0\)つまり\(0<\zeta<1\)のとき不足減衰(Underdamped)
\(0<\zeta<1\)のときシステムの極\(s_1,s_2\)は
\(s_1 = -\zeta\omega_n + j\omega_n \sqrt{1-\zeta^2}\),\(s_2 = -\zeta\omega_n – j\omega_n \sqrt{1-\zeta^2}\)となる.
このとき\(s_1,s_2\)は実部が負の複素数となり振動子ながら減衰する.
\(\omega_n<-\zeta \omega_n<0\)より臨界減衰よりもゆっくりと減少することがわかる.
特に\(\zeta<\frac{1}{\sqrt{2}}\)のときゲイン線図に共振ピークが現れる
\begin{align}
20\log_{10} |G(j\omega)| &= 20\log_{10} \frac{K\omega_n^2}{ \sqrt{(2\zeta\omega_n \omega)^2+(\omega_n^2 – \omega^2)^2}}\\
&= 20\log_{10} K\omega_n^2 -20\log_{10}\sqrt{(2\zeta\omega_n \omega)^2+(\omega_n^2 – \omega^2)^2}
\end{align}
一項目は定数のため,共振ピークが現れるかどうかは2項目のルートの中身が単調に増加するか,減少→増加となるかによる.つまり
\begin{align}
(2\zeta\omega_n \omega)^2+(\omega_n^2 – \omega^2)^2 &= 4\zeta^2\omega_n^2 \omega^2+ \omega^4 – 2\omega_n^2\omega^2 + \omega_n^4\\
&= \omega^4 + 2(2\zeta^2 – 1)\omega_n^2\omega^2 + \omega_n^4\\
&= (\omega^2 – (1-2\zeta^2)\omega_n^2)^2 – ((1-2\zeta^2)\omega_n^2)^2 + \omega_n^4
\end{align}
より\(\zeta<\frac{1}{\sqrt{2}} \simeq 0.7071\)のとき\(\omega = \sqrt{1-2\zeta^2}\omega_n\)にピークを持つ.
イメージ(\(\omega_n = 3\))のとき
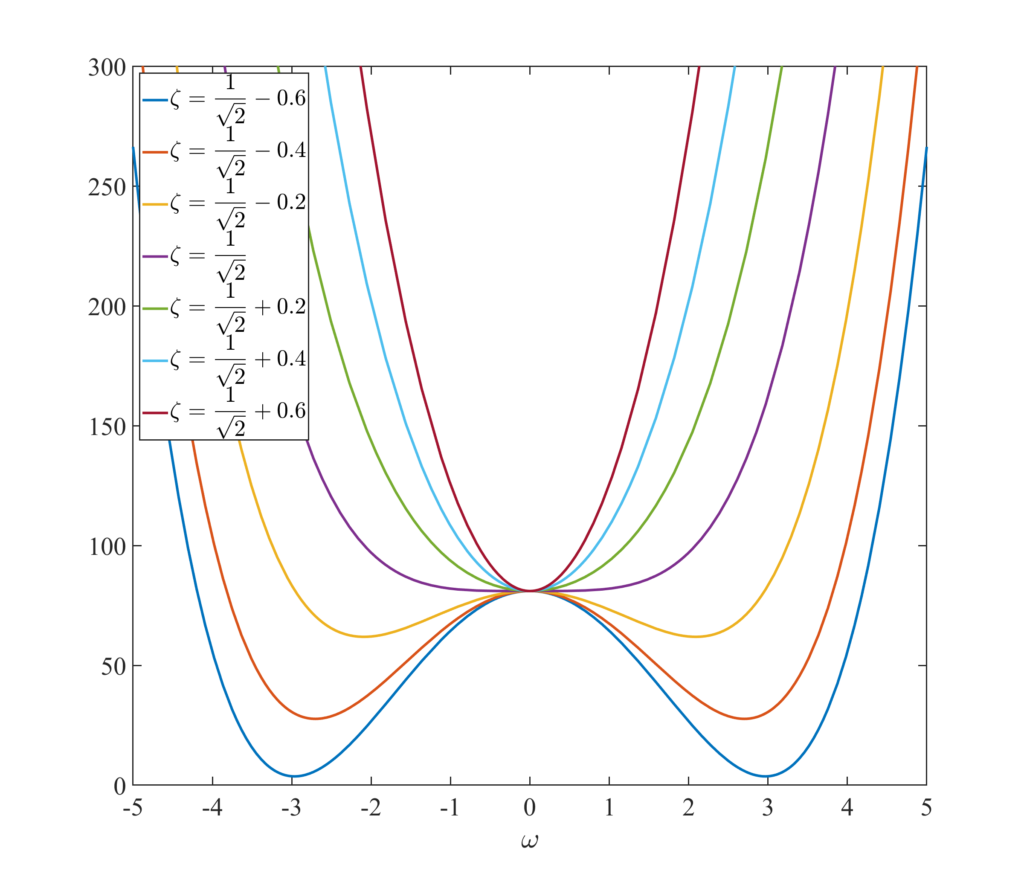
\(\zeta=0\)のとき不減衰(Undamped)
\(\zeta>1\)のときシステムの極\(s_1,s_2\)は
\(s_1 = j\omega_n\),\(s_2 = – j\omega_n \)の純虚数となる.
このときシステムのインパルス応答は減衰せず振動が永遠に続く.
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010.




ディスカッション
コメント一覧
まだ、コメントがありません