生物工学演習E -第6回- 離散時間フーリエ変換
今回の概要
離散時間フーリエ変換の(連続時間)フーリエ変換からの導出
離散信号のフーリエ変換が周波数領域で周期的になること,周期信号のフーリエ変換(フーリエ級数展開)が周波数領域で離散的になることを理解する.
離散時間フーリエ変換
離散時間フーリエ変換
\begin{align}
X(\tilde{\omega})= \sum_{n=-\infty}^{\infty} x_n e^{-j\tilde{\omega} n}
\end{align}
離散時間フーリエ逆変換
\begin{align}
x_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} X(\tilde{\omega}) e^{j\tilde{\omega} n} d\tilde{\omega}
\end{align}
(連続時間)フーリエ変換
\begin{align}
X(\omega)= \int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt
\end{align}
(連続時間)フーリエ逆変換
\begin{align}
x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\omega) e^{j\omega t} d\omega
\end{align}
連続時間と離散時間のフーリエ変換で異なる点は大きく3つある.
一つ目は角周波数が正規化角周波数\(\tilde{\omega} = \omega T_s = 2\pi f T_s\)になっている点.
二つ目は変換する際の積分が和になっている点.
三つ目は逆変換の際に積分範囲が\(\pm \infty\)から\(\pm \pi\)になっている点である.
離散時間フーリエ変換の導出
まず,離散時間信号\(x_n\)をそのままフーリエ変換することを考える.
しかし,離散時間信号をある点でのみ値をもつ関数と考えるとその積分は0になってしまう.
そこで\(x_n\)にそれぞれディラックのデルタ関数をかけた信号\(x_n(t)=\sum_{n=-\infty}^{\infty}x_n \delta(t- T_s n)\)をフーリエ変換することを考える.ここで\(T_s\)はサンプリング間隔を表す.
実際に計算すると
\begin{align}
X(\omega)&= \int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt\\
&= \int_{-\infty}^{\infty} \sum_{n=-\infty}^{\infty}x_n \delta(t-T_s n) e^{-j\omega t} dt\\
&= \sum_{n=-\infty}^{\infty}x_n \int_{-\infty}^{\infty}\delta(t-T_s n) e^{-j\omega t} dt\\
&= \sum_{n=-\infty}^{\infty}x_n e^{-j\omega T_s n}\\
X(\tilde{\omega} )&= \sum_{n=-\infty}^{\infty}x_n e^{-j\tilde{\omega} n}
\end{align}
離散時間信号をある点でのみ値をもつ関数と考えるとその積分は0になってしまう.
そこで離散時間信号に幅を持たせた階段状の信号を積分するという考え方もある.
この信号の面積は各短冊の和に等しいので以下のように書ける.
\begin{align}
X(\tilde{\omega})= \sum_{n=-\infty}^{\infty} x(n) e^{-j\tilde{\omega} n} dt
\end{align}
これが離散時間フーリエ変換の定義である.
このとき正規化角周波数\(\tilde{\omega} = \omega T_s = 2\pi f T_s\)が使用されている理由は1サンプルごとにどれだけ角周波数が進むかを表す\(\tilde{\omega}\)にサンプル番号\(n\)をかけた値が連続時間における\(\omega t\)に対応するからである.
離散時間フーリエ変換では周波数領域は周期的になる
離散時間信号\(x_n\)にディラックのデルタ関数をかけた信号は
\begin{align}
x_n(t)&=\sum_{n=-\infty}^{\infty}x_n \delta(t- T_s n)\\
&=x(t)\sum_{n=-\infty}^{\infty} \delta(t- T_s n)
\end{align}
のように連続時間信号\(x(\cdot)\)にくし型関数をかけた信号としても考えられる.
以下では関数の積のフーリエ変換が畳み込み積分で表せることを利用して離散時間フーリエ変換の結果が周波数領域で周期的になることを示す.
まず,関数の積のフーリエ変換がそれぞれをフーリエ変換したものの畳み込み積分で表せることを示す.
\begin{align}
\mathscr{F}[x(t)y(t)]&= \int_{-\infty}^{\infty} x(t)y(t) e^{-j\omega t} dt\\
&= \int_{-\infty}^{\infty} y(t)\left [\frac{1}{2\pi} \int_{-\infty}^{\infty} X(\omega’) e^{j\omega’ t} d\omega’ \right ] e^{-j\omega t} dt\\
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\omega’) \left [\int_{-\infty}^{\infty} y(t)e^{-j\omega t}e^{j\omega’ t} dt \right ] d\omega’\\
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\omega’) \left [\int_{-\infty}^{\infty} y(t)e^{-j(\omega-\omega’) t}dt \right ] d\omega’\\
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} X(\omega’) Y(\omega-\omega’) d\omega’\\
&= \frac{1}{2\pi} (X*Y)(\omega)
\end{align}
つまり,離散時間信号のフーリエ変換は\(\mathscr{F}[x_n(t)]=\mathscr{F}\left [x(t)\sum_{n=-\infty}^{\infty} \delta(t- T_s n) \right ]\)となるので周波数領域では\(X(\omega)\)と\(\mathscr{F}\left [\sum_{n=-\infty}^{\infty} \delta(t- T_s n) \right ](\omega)\)の畳み込み積分で表現される.
くし型関数はフーリエ変換してもくし型関数になるという性質を持つ.
具体的には\(\mathscr{F}\left [\sum_{n=-\infty}^{\infty} \delta(t- T_s n) \right ](\omega)\)は幅\(\frac{2\pi}{T_s}\)のくし型関数となる.
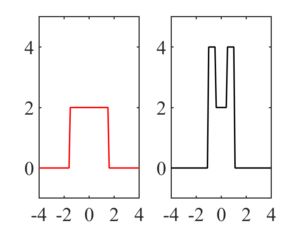
そして周波数領域において任意の連続時間信号(例として矩形波)とくし型関数との\(X(\omega)\)の畳み込み積分は動画のようになり,離散時間フーリエ変換は周波数領域で周期的になることがわかる.
このとき,元の信号の周波数帯域幅がくし形関数の幅よりも広い場合は周波数領域において,元の連続信号が持っていた周波数の情報が一部失われ,ナイキスト周波数で折り返した周波数をもつ信号と区別できなくなる.
上記のような状況では離散化前の連続信号の周波数か以下のどちらだったのか区別できない.
離散時間逆フーリエ変換の確認
今回は離散時間逆フーリエ変換の式に,変換の式を入れることで天下り的に確認する.
がこれも結局内積計算だと考えると忘れてしまっても問題なく導出できると思われる.
\begin{align}
x_n &= \frac{1}{2\pi} \int_{-\pi}^{\pi} X(\tilde{\omega}) e^{j\tilde{\omega} n} d\tilde{\omega}\\
&= \frac{1}{2\pi} \int_{-\pi}^{\pi} \sum_{n’=-\infty}^{\infty} x_{n’} e^{-j\tilde{\omega} n’} e^{j\tilde{\omega} n} d\tilde{\omega}\\
&= \frac{1}{2\pi} \sum_{n’=-\infty}^{\infty} \int_{-\pi}^{\pi} x_{n’} e^{-j\tilde{\omega} (n’-n)} d\tilde{\omega}\\
&= \frac{1}{2\pi} (\cdots+0+0+2\pi x_{n}+0+0+\cdots)\\
&= x_{n}
\end{align}


ディスカッション
コメント一覧
まだ、コメントがありません