生物工学演習D -第9回- 比例・積分・微分制御(PID制御)
今回の目標
□比例制御器,積分制御器,微分制御器の特徴と役割を理解する
制御システム
フィードフォワード(FF)制御

フィードバック(FB)制御
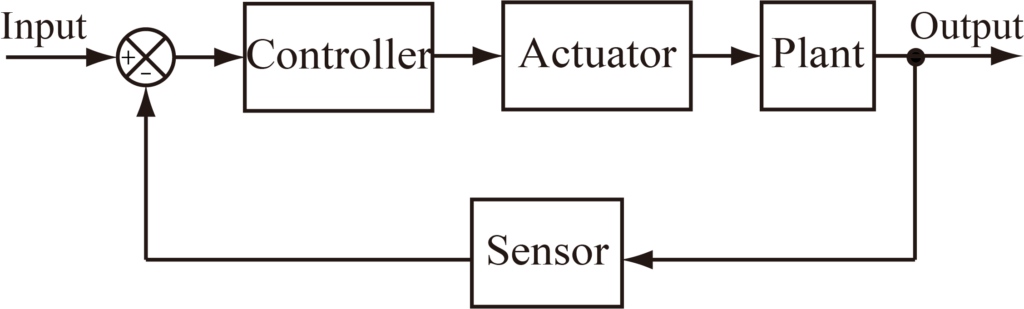
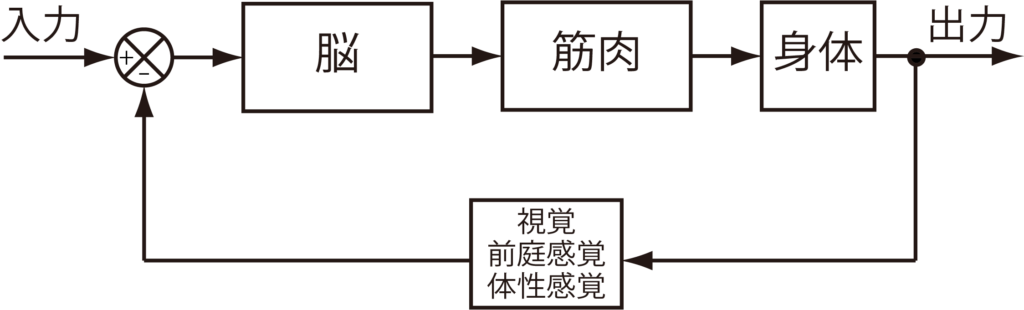
制御器の特徴
比例制御器
フィードバック制御の基本的な手法
制御対象によっては目標値に完全に一致させられず定常偏差が生じる可能性がある
微分制御器
偏差の微分に基づいて操作量を決定する手法
動特性の改善(振動の減少)に用いられる.定常偏差を減らす能力はない.
積分制御器
偏差の累積に基づいて操作量を決定する手法
目標値に一致するように働くが定常状態に達するまでに時間がかかる.システムの不安定化の原因にもなる.
例

比例制御
制御器が比例制御器のとき,伝達関数\(G(s)\)は
\begin{align}
G(s) &= \frac{K_p\frac{1}{ms^2+bs+k}}{1 + K_p\frac{1}{ms^2+bs+k}}\\
&= \frac{K_p}{ms^2+bs+ (k + K_p)}
\end{align}
このシステムの単位ステップ入力\(u(t)\)に対する応答を考えると
\begin{align}
X(s) &= \frac{K_p}{ms^2+bs+ (k + K_p)}\frac{1}{s}\\
&=\frac{K_p}{k+K_p}\left(\frac{1}{s} – \frac{ms+b}{ms^2 + bs + (k+K_p)}\right)\\
&=\frac{K_p}{k+K_p}\left(\frac{1}{s} – \frac{s+\frac{b}{2m}+\frac{b}{2m}}{(s + \frac{b}{2m})^2 -(\frac{b}{2m})^2 + (k+K_p)}\right)\\
&=\frac{K_p}{k+K_p}\left(\frac{1}{s} – \frac{s+\frac{b}{2m}}{(s + \frac{b}{2m})^2 + \omega_n^2} – \frac{\frac{b}{2m}}{(s + \frac{b}{2m})^2 + \omega_n^2}\right)
\end{align}
例として\(\omega_n = \sqrt{\frac{k+K_p}{m}-(\frac{b}{2m})^2} \in R\)と仮定すると
\begin{align}
x(t) &=\frac{K_p}{k+K_p}\left(1- e^{-\frac{b}{2m}t} (\cos \omega_n t + \alpha \sin \omega_n t)\right)
\end{align}
ただし\(\alpha = \frac{b}{2m\omega_n}\).
このとき\(t\rightarrow \infty \)で\(x(\infty)=\frac{K_p}{k+K_p}\).つまり定常状態において目標値と一致していないことに注意.このような定常状態における誤差を定常偏差と呼ぶ.
比例積分制御
比例制気分制御は上記の定常偏差を減らすことができることを確認する.
比例積分制御では制御器の伝達関数は\(C(s) = K_P + \frac{K_I}{s}\)となる.
つまりシステム全体の伝達関数\(G(s)\)は
\begin{align}
G(s) &= \frac{(K_P + \frac{K_I}{s})\frac{1}{ms^2+bs+k}}{1 + (K_P + \frac{K_I}{s})\frac{1}{ms^2+bs+k}}\\
&= \frac{K_P s + K_I}{s(ms^2+bs+k) + (K_P s + K_I)}\\
&= \frac{K_P s + K_I}{ms^3+bs^2+(k + K_P) s + K_I}
\end{align}
このシステムの単位ステップ応答を考えると
\begin{align}
X(s) &= \frac{K_P s + K_I}{ms^3+bs^2+(k + K_P) s + K_I}\frac{1}{s}\\
&= \frac{K_P s + K_I}{ms^3+bs^2+(k + K_P) s + K_I}\frac{1}{s}\\
&= \frac{1}{s} – \frac{ms^2+bs+k}{ms^3+bs^2+(k + K_P) s + K_I}\\
&= \frac{1}{s} – \frac{a}{s+\alpha} – \frac{bs+c\omega_n}{(s+\beta)^2+\omega_n^2}
\end{align}
よって逆ラプラス変換すると
\begin{align}
x(t) &= 1 – e^{-\alpha t} – e^{-\beta t}(b\cos \omega_n t + c\sin \omega_n t)
\end{align}
このとき定常状態\((t\rightarrow\infty)\)では\(x(t)=1\)となり目標値と一致していることがわかる.
最終値の定理
最終値の定理を用いるとシステムの伝達関数から定常偏差を計算することができる.
\begin{align}
\lim_{t \rightarrow \infty} e(t) &= \lim_{s \rightarrow 0} sE(s)
\end{align}
誤差\(e(t) = u(t) – x(t)\)とする.このとき誤差の導関数\(\frac{d}{dt}e(t)\)のラプラス変換は
\begin{align}
\int_0^\infty \frac{d}{dt}e(t) e^{-st} dt &= sE(s) – e(0)
\end{align}
両辺に対して\(s\rightarrow0\)の極限を考えると
\begin{align}
\lim_{s \rightarrow 0}\int_0^\infty \frac{d}{dt}e(t) e^{-st} dt &= \lim_{s \rightarrow 0}(sE(s) – e(0)) \\
\int_0^\infty \frac{d}{dt}e(t)dt &= \lim_{s \rightarrow 0}(sE(s)) – e(0)\\
[e(t)]_0^\infty &= \lim_{s \rightarrow 0}(sE(s)) – e(0)\\
e(\infty)-e(0) &= \lim_{s \rightarrow 0}(sE(s)) – e(0)\\
e(\infty) &= \lim_{s \rightarrow 0}sE(s)
\end{align}
また,最終値の定理はヘビサイド展開定理で1/sの項の係数を求める手順とほとんど同じことをしている.
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p567-



ディスカッション
コメント一覧
まだ、コメントがありません