生物工学演習E -第1回- ベクトルと関数の内積・直交
今回の目標
ベクトルおよび関数の内積,基底ベクトル(関数),直交性,ノルムを理解する.
信号解析論とは
本演習では時間的,もしくは空間的に変化する物理量を信号と呼ぶ.例えば脳波や筋電図,音,画像などである.
生体信号など様々な信号を取り扱う際,その信号の周波数解析やノイズのフィルタリング,データの圧縮などを行う機会がある.本演習では演習問題を通して以下のキーワードを感覚的に友人に説明できる程度に理解することを目指す.そのため,数学的厳密性については他の講義にゆずる.
キーワード:内積,直交,フーリエ級数展開,フーリエ変換,サンプリング定理,離散時間フーリエ変換,離散フーリエ変換,ラプラス変換,Z変換,デジタルフィルタ,確率過程,相関関数
信号と関数,ベクトル
本演習では様々な信号を扱う.
まず信号を大きく分けると時間が連続な連続時間信号と離散な離散時間信号に分けることができる.
そして以下の図のように連続時間信号は関数\(f(\cdot)\),離散時間信号はベクトル\(\boldsymbol{v}\)で表現できる.
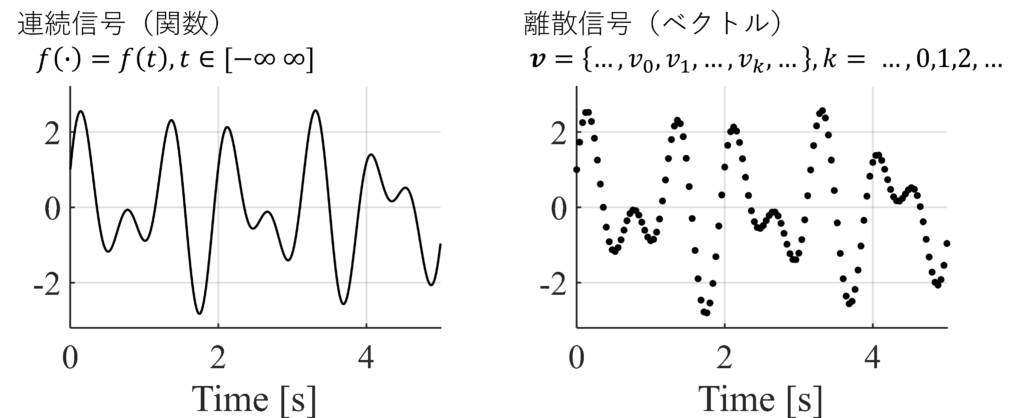
また,離散信号の時間ステップ\(\Delta t\)を0に近づけていくと,その極限は関数が表している情報とほぼ同じになる.
何が言いたいかというと"関数"と"ベクトル"というものは実は非常に近い性質をもつ似た存在であるということである.
より詳細を知りたい方は関西大学の岡村隆先生が公開されているpdf"関数としてのベクトル, ベクトルとしての関数“を読んでいただくのが良いと思う.
詳細な説明は上記の文献にゆずり,ここでは簡単に関数とは,ベクトルとは何だったのかを定義から簡単に振り返り,関数は無限次元のベクトルであるということを感覚的に納得してもらうことを目指す.
関数の定義
\(X\),\(Y\)を集合とするとき\(X\)の任意の要素\(x\)に対して,\(Y\)の要素\(y\)を一意に定める規則\(f\)が与えられているとき,\(f\)のことを\(X\)から\(Y\)への写像(関数)といい,
\begin{align}
f : X \to Y
\end{align}
と記す.
例えば本演習で扱う信号の場合,関数\(f\)は時間の集合\(\{t\}\)からその時刻の信号の値の集合\(\{y\}\)への写像である.
ベクトル空間の定義
加法とスカラー倍が定義された集合をベクトル空間と呼び,その要素をベクトルという.
おおざっぱにいうと要素間での足し算と定数倍の掛け算がいい感じに定義されている空間だと考えてほしい.
例えば関数\(f(t)\)と\(g(t)\),\(h(t)\)を考えた際に
\begin{align}
f(t) + g(t) &= g(t) + f(t) \qquad (\text{可換則})\\
(f(t) + g(t)) + h(t) &= g(t) + (f(t)+h(t)) \qquad (\text{結合則})\\
\alpha(f(t) + g(t)) &= \alpha f(t) + \alpha g(t) , \alpha \in \mathbb{C}
\end{align}
等(満たすべき性質は上記以外にももう少しある)の性質が満たされそうなことはイメージしてもらえるのではないかと思う.
つまり,ベクトルをその機能に着目して加法とスカラー倍が定義された集団の要素としたとき,関数の集合も数字を並べたベクトルと同様にそれを満たすことができそうだなと感じてほしい.
関数は無限次元ベクトル
ベクトルの場合\(n\)個の数字が並んだものを\(n\)次元ベクトルと呼んだのだった,関数の場合はどうだろうか?
有限の区間を考えた場合でも関数の場合,無限に数字を並べることになる.
例えば\(f(0.24)\)と\(f(0.25)\)の間には\(f(0.241)\)があるし,さらにその間に\(f(0.2401)\)といった感じでいくらでも数字を並べることができる(書ききることはできない).
線形代数でベクトルについて学んだと思うが,無限次元のベクトルとみなせる関数は関数解析学(線形代数の無次元版)で研究されている.
それについては河東康之先生(東京大学大学院数理科学研究科)による文章"無限次元“と"線形代数と関数解析学 — 無限次元の考え方“を読むと歴史的なながれ,無限次元になることによる違いと共通の性質について少しイメージが持てるようになると思われる.
ベクトルおよび関数の内積と類似性の計算
内積と聞くと以下のまずはベクトルの内積が思い浮かぶのではないだろうか.
実ベクトルの内積
2つの実ベクトル\(\boldsymbol{a}\)と\(\boldsymbol{b}\)を考えるとそれらの内積は
\begin{align}
\langle \boldsymbol{a}, \boldsymbol{b} \rangle &= \boldsymbol{a}^T \boldsymbol{b}\\
&=\sum_{k=-\infty}^{\infty} a_kb_k\\
&=\|\boldsymbol{a}\|\|\boldsymbol{b}\|\cos(\theta)
\end{align}
のように様々な表現ができる.\(\|\boldsymbol{a}\|\)はベクトル\(\boldsymbol{a}\)の大きさを表す量でノルムとよばれ,同じベクトル同士の内積の平方根\(\sqrt{\langle \boldsymbol{a}, \boldsymbol{a} \rangle}\)で定義される.
内積の結果わかることとして類似性がある.
つまり,似たようなベクトルの内積の絶対値は大きくなり,異なるベクトルの間の内積は0に近づくのである.
本当だろうか?いくつか試してみてほしい.
例えば極端な例として
縦ベクトル\(\boldsymbol{a} = (0,1,1)^T\)と\(\boldsymbol{b} = (0.5,0.5,0)^T\)の内積は
\begin{align}
\langle \boldsymbol{a}, \boldsymbol{b} \rangle & = 0\times 0.5+1\times 0.5+1\times 0 = 0.5
\end{align}
となるが\(\boldsymbol{c} = (0,0.5,0.5)^T\)との内積は
\begin{align}
\langle \boldsymbol{a}, \boldsymbol{c} \rangle & = 0\times0+1\times 0.5+1\times 0.5 = 1
\end{align}
となり,似ているベクトル同士の内積が大きくなっている.
ただこのベクトル\(\boldsymbol{b}\)と\(\boldsymbol{c}\)で内積の大きさを比較できるのは両者のベクトルの大きさ(ノルム)が同じだからである.
ノルムが異なる場合には両ベクトルのノルム\(\|\boldsymbol{a}\|\|\boldsymbol{b}\|\)もしくは\(\|\boldsymbol{a}\|\|\boldsymbol{c}\|\)で割り規格化した方向余弦\(\cos \theta\)の大きさを比べる必要がある.
実関数の内積
実は関数も同様に内積を考えることができる.
定義域が\([d_1 d_2]\)である実関数\(f(\cdot)\)と\(g(\cdot)\)の内積は積分を使って次のように定義できる.
\begin{align}
\langle f, g \rangle & = \int_{d_1}^{d_2}f(t)g(t)dt
\end{align}
関数の内積もベクトルと同様に,対象とした2つの関数の類似度により大小が変化し,0のとき類似度が一番小さい(直交).
ノルムもベクトルの場合と同様に内積の平方根\(\sqrt{\langle f, f \rangle}\)で定義できる(これはL2ノルムと呼ばれる).
(注)ここでは内積を定義するにあたり,和や積分が有限の値となるベクトルや関数を前提としているが,そうではないものもたくさんある.
基底ベクトル,基底関数と直交
通常あるベクトルを以下のようにほかのベクトルの線形和で表すことができる.
例えば2次元ベクトルの場合は,2つの1次独立なベクトル\(\boldsymbol{b}_1, \boldsymbol{b}_2\)を使って任意のベクトル\(\boldsymbol{a}\)を線形和で表現できる.
\begin{align}
\boldsymbol{a} & = k_1 \boldsymbol{b}_1 + k_2 \boldsymbol{b}_2
\end{align}
このとき\(\boldsymbol{b}_1, \boldsymbol{b}_2\)を基底ベクトルと呼ぶ.
n次元ベクトルの基底ベクトルはn個必要となる.
同様に基底関数というものも考えることができて,基底関数の線形和としてほかの関数を表すことができる.
今後でてくるフーリエ級数展開などではこの基底関数同士が直交していることが重要である.
まとめと今回のイメージ
- 関数は無限次元ベクトル
- 関数とベクトルの両方に対して内積,ノルムが定義できる
- 任意の\(n\)次元ベクトルを\(n\)個の基底ベクトルで表現できるように,関数を基底関数の和として表すこともできる
補足
感覚をつかむことを優先したため,数学的厳密性については足りない部分があると思われる.気になる点があればコメントでご指摘ください.


ディスカッション
コメント一覧
まだ、コメントがありません