生物工学演習E -第2回- 周期信号に対するフーリエ級数展開
今回の目標
連続時間周期信号をフーリエ級数展開できるようになる.
周期信号とは
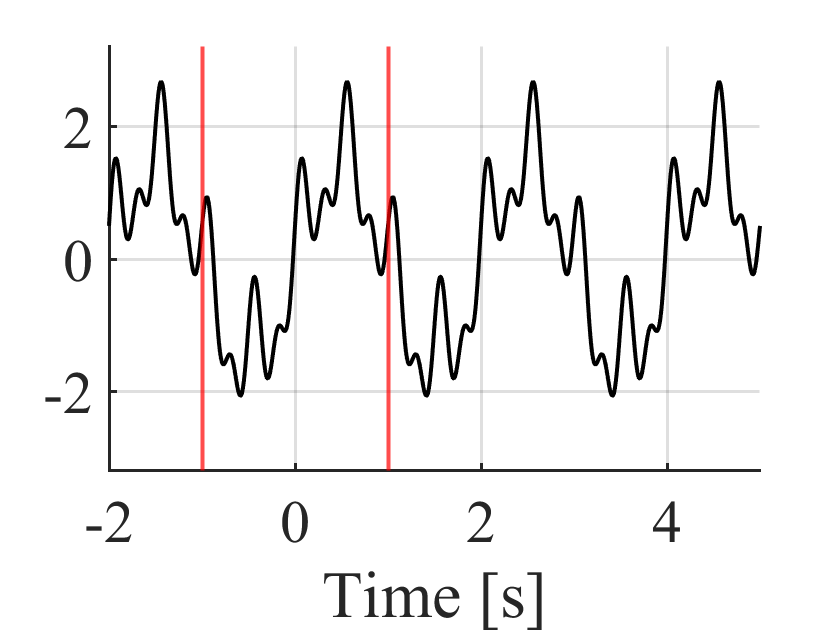
今回は周期信号\(x(\cdot)\)を考える.
\(x(\cdot)\)が周期\(T\)の周期信号の場合,\(x(t+nT) = x(t)\)となる.
今回はこの周期Tで繰り返される周期信号を三角関数の和に分解するフーリエ級数展開について学ぶ.
三角関数は基底関数として良い性質(直交性)をもつ
三角関数を集めた関数系{\(1, \sin \omega_0 t,\cos \omega_0 t, \sin 2\omega_0 t,\cos 2\omega_0 t,\dots \)}は直行基底関数系となる.ここで\(\omega_0 = \frac{2\pi}{T}\).
例えば\(t \in [-T/2,T/2]\)で定義された\(\sin m \omega_0 t\)と\(\cos n \omega_0 t\)の内積は以下のように0になる.ここで\(m\)と\(n\)は自然数.
\begin{align}
&\langle \sin m \omega_0 t, \cos n \omega_0 t \rangle \\
&= \int_{-T/2}^{T/2}\sin m \omega_0 t \cos n \omega_0 t dt\\
& = \int_{-T/2}^{T/2} \frac{1}{2} ( \sin (m+n) \omega_0 t + \sin (m-n) \omega_0 t )dt\\
& = \frac{1}{2} \left [( -\frac{1}{(m+n)\omega_0}\cos (m+n) \omega_0 t + -\frac{1}{(m-n)\omega_0}\cos (m-n) \omega_0 t ) \right]_{-T/2}^{T/2}
\end{align}
このとき,\(\cos (m+n) \omega_0 T/2 = \cos (m+n) \frac{2\pi}{T} T/2 = \cos \pi(m+n)=-1 \),
同様に\(\cos (m+n) \omega_0 (-T/2) = \cos (m+n) \frac{2\pi}{T}(- T/2) = \cos -\pi(m+n)=-1 \)である.
これは2項目についても成り立って\(\cos (m-n) \omega_0 (\pm T/2) =-1 \).
つまり上記の内積は
\begin{align}
&\langle \sin m \omega_0 t, \cos n \omega_0 t \rangle \\
& = \frac{1}{2} \left [( -\frac{1}{(m+n)\omega_0}\cos (m+n) \omega_0 t + -\frac{1}{(m-n)\omega_0}\cos (m-n) \omega_0 t ) \right]_{-T/2}^{T/2}\\
& = \frac{1}{2} \left (( -\frac{1}{(m+n)\omega_0}(-1+1) + -\frac{1}{(m-n)\omega_0}(-1+1) ) \right)\\
& = 0
\end{align}
となる.
上の計算では\(m\neq n\)の場合を考えているが\(m=n\)の場合には2項目が0となる以外は同様の計算で内積が0となることが確認できる.
つまり,\(\sin m \omega_0 t\)と\(\cos n \omega_0 t\)は直交している.
実は\(\sin m \omega_0 t\)と\(\sin n \omega_0 t\),\(\cos m \omega_0 t\)と\(\cos n \omega_0 t\)の組み合わせについても\(m \neq n\)のとき内積が0,つまり直交しているので,その計算は演習問題で各自確認してほしい.
フーリエ係数の計算は周期関数と三角関数系との内積計算
さて関数系{\(1, \sin \omega_0 t,\cos \omega_0 t, \sin 2\omega_0 t,\cos 2\omega_0 t,\dots \)}, \(t \in [-T/2,T/2]\)が直交関数系となりそうなことを確認した.
これらを基底関数としてある周期関数\(x(\cdot)\)を線形和で表せると仮定してみよう.
すると以下のように係数\(a_k,b_k\)を使って表せると仮定することになる.
\begin{align}
x(t) \sim a_0\times 1 + \sum_{k=1}^{\infty}\{a_k \cos(k\omega_0 t) + b_k \sin(k\omega_0 t)\}
\end{align}
ここで\(\omega_0 = \frac{2\pi}{T}\)である.
このとき,各係数\(a_0,a_k,b_k\)はどのように求めればよいだろうか.
ここで直交な基底関数を選んだことが生きてくる.
基底関数系{\(1, \sin \omega_0 t,\cos \omega_0 t, \sin 2\omega_0 t,\cos 2\omega_0 t,\dots \)}は直交なので内積を計算すると対応する基底関数に関する項しか残らない.
例えば \(x(t)\)と\(\cos 2\omega_0 t\)との内積を計算してみると
\begin{align}
&\langle x(t), \cos 2 \omega_0 t \rangle \\
&= \int_{-T/2}^{T/2} x(t) \cos 2 \omega_0 t dt\\
& = \int_{-T/2}^{T/2} \left (a_0\times 1 + \sum_{k=1}^{\infty}\{a_k \cos(k\omega_0 t) + b_k \sin(k\omega_0 t)\}\right ) \cos 2 \omega_0 t dt\\
& = 0 + 0 + \dots + 0 + \int_{-T/2}^{T/2} \left (a_2 \cos(2\omega_0 t) \right ) \cos 2 \omega_0 t dt + 0 + \dots + 0\\
& = a_2\int_{-T/2}^{T/2} \left (\cos(2\omega_0 t) \right ) ^2 dt \\
& = a_2 \int_{-T/2}^{T/2} \frac{1}{2}\left (\cos(4\omega_0 t) +1 \right ) dt \\
& = a_2 \left[\frac{1}{2\times 4 \omega_0}\sin(4\omega_0 t) +\frac{1}{2}t \right ]_{-T/2}^{T/2}\\
& = a_2 (0 +\frac{1}{2}(\frac{T}{2}-\frac{-T}{2}) \\
& = a_2 \frac{T}{2}
\end{align}
つまり,\(a_2 = \frac{2}{T}\int_{-T/2}^{T/2} x(t) \cos 2 \omega_0 t dt\)である.
内積とノルム\(\|g\|=\sqrt{\langle g, g \rangle}\)を使って書くと\(a_2 = \frac{1}{\|\cos 2 \omega_0 t\|^2}\langle x(t), \cos 2 \omega_0 t \rangle \)と表せる.
同様に内積とノルムによってすべての係数を求めることができて,
\begin{align}
a_0&=\frac{1}{\|1\|^2}\langle x(t), 1 \rangle \\
&= \frac{1}{T}\int_{-T/2}^{T/2} x(t) \times 1 dt\\
a_k&=\frac{1}{\|\cos k \omega_0 t\|^2}\langle x(t), \cos k \omega_0 t \rangle \\
&= \frac{2}{T}\int_{-T/2}^{T/2} x(t) \cos k \omega_0 t dt\\
b_k&=\frac{1}{\|\sin k \omega_0 t\|^2}\langle x(t), \sin k \omega_0 t \rangle \\
&= \frac{2}{T}\int_{-T/2}^{T/2} x(t) \sin k \omega_0 t dt\\
\end{align}
フーリエ級数の収束の条件
さらっと流したので気づかなかったかもしれないが,無限級数において積分と総和の入れ替えが常にできるわけではない…
だが実用上多くの関数に対して収束することが知られている.
ディリクレが証明したディリクレ条件というものがあり,区分的に滑らか(piecewise smooth)な関数\(x(\cdot)\)で\(x(\cdot)\)のフーリエ級数展開が\(x(\cdot)\)に各点収束することが知られている.
直観的には関数の一周期分のグラフが有限の長さを持てば,フーリエ級数が収束することが知られている.
収束しない例としては\(\tan t\)などがある.このように不連続点において値が無限大に発散するような関数は収束しない.
関数\(x(\cdot)\)が区分的に滑らかであるとは,関数\(x(\cdot)\)が区分的に連続であり,さらにその導関数\(x'(\cdot)=\frac{dx}{dt}\)がさらに区分的に連続であることである.
区分的に連続(piecewise continuous)とは有限個の点を除いて連続で,その有限個の不連続点において右からの極転置と左からの極限値が存在して,有限の値が存在することである.
不連続点\(a\)における右からの極限値は
\begin{align}
\lim_{\epsilon \to 0}x(a+\epsilon), (\epsilon >0)
\end{align}
左からの極限は
\begin{align}
\lim_{\epsilon \to 0}x(a-\epsilon), (\epsilon >0)
\end{align}
参考文献
[1] タンジェントのフーリエ級数について
新潟工科大学の竹野茂治先生によるタンジェントのフーリエ級数展開の解説pdf


ディスカッション
コメント一覧
まだ、コメントがありません