生物工学演習E -第4回- 非周期信号に対するフーリエ変換

2023-09-262023-11-06

今回の目的

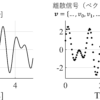
非周期信号に対するフーリエ変換を身につける．

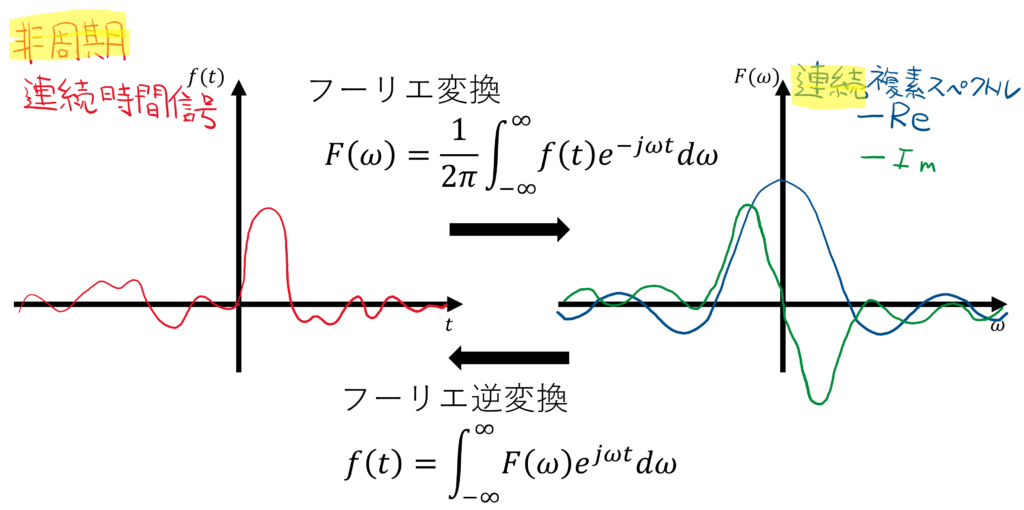
周期\(T\)の極限によるフーリエ級数展開からフーリエ変換の導出

前回，以下の周期\(T\)の信号\(x(\cdot)\)に対する複素フーリエ級数展開を行った．

\begin{align}
x(t) = \sum_{k=-\infty}^{\infty}X_k e^{j\omega_k t}
\end{align}

ここで\(\omega_k = \frac{2\pi}{T}k\)である．

このときフーリエ係数は以下の内積の結果，複素数として得られる．

\begin{align}
X_k &= \frac{1}{T}\int_{-T/2}^{T/2} x(t) \times e^{-j\omega_k t} dt
\end{align}

今回は周期\(T\)を無限大にすることによって，非周期信号を波に分解するフーリエ変換について考える．

複素フーリエ級数展開において\(\lim_{T \to \infty}\)をとり，少し変形すると

\begin{align}
x(t) &= \lim_{T \to \infty} \sum_{k=-\infty}^{\infty}X_k e^{j\frac{2\pi}{T}k t}\\
&= \lim_{T \to \infty} \sum_{k=-\infty}^{\infty}\frac{T}{2\pi} X_k e^{j\frac{2\pi}{T}k t} \frac{2\pi}{T}\\
&= \lim_{n \to \infty} \sum_{k=-\infty}^{\infty} n X_k e^{j\frac{k}{n} t} \frac{1}{n}\\
&= \lim_{n \to \infty} \sum_{k=-\infty}^{\infty} g\left (\frac{k}{n} \right ) \frac{1}{n}\
\end{align}

であるが実はこの極限と和という形は区分求積法の考え方で積分にすることができる．

上記の式中では

\begin{align}
\frac{1}{n} &=\frac{2\pi}{T} = \Delta \omega ，\\
g\left (\omega_k \right ) &= \frac{k}{\omega_k} X_k e^{j\omega_k t}\\
&= \frac{kT}{2\pi k} \frac{1}{T}\int_{-T/2}^{T/2} x(t) e^{-j\omega_k t} dt \times e^{j\omega_k t}\\
&= \frac{1}{2\pi}\int_{-T/2}^{T/2} x(t) e^{-j\omega_k t} dt \times e^{j\omega_k t}\\
\end{align}

とした．

区分求積法の復習

高校の数Ⅲで学んだ区分求積法は以下のようなものだった．（ここでは積分と和の極限の関係のイメージを思い出してもらうことを目的とし，あまり厳密な議論は行わない．）

\begin{align}
\lim_{n \to \infty} \sum_{k=0}^{n-1}f\left( \frac{k}{n} \right) \frac{1}{n} &= \int_{0}^{1} f(x) dx
\end{align}

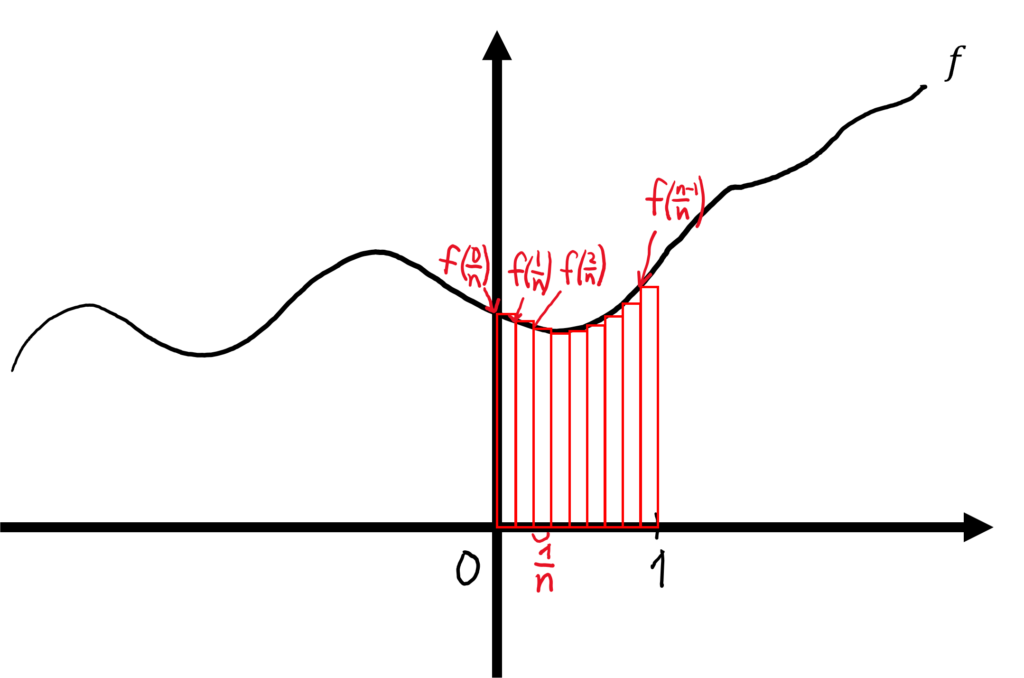
図を見てもらうと良いのだがこれは0から1の範囲で関数\(f\)を幅\(\frac{1}{n}\)の\(n\)個の短冊に分解したものの和の極限をとったものである．

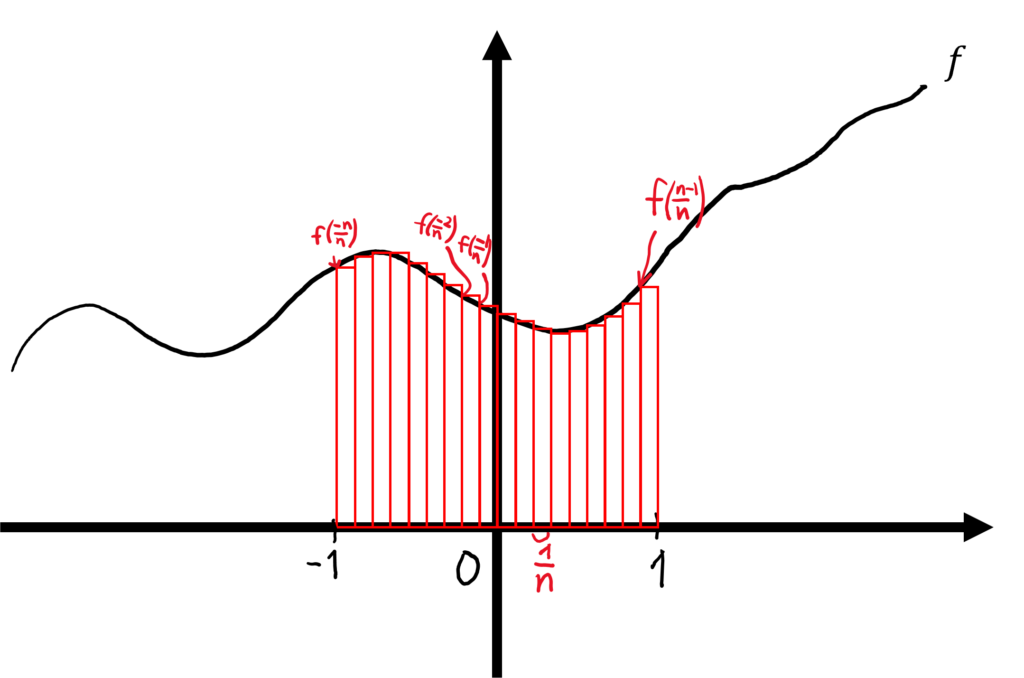
では，積分範囲が区間[-1,1]のとき和の範囲はどのようになるだろうか．この場合以下の図のように短冊を作成することになる．この時関数\(f\)の引数に注意すると総和\(\sum\)の範囲が変化し，

\begin{align}
\lim_{n \to \infty} \sum_{k=-n}^{n-1}f\left( \frac{k}{n} \right) \frac{1}{n} &= \int_{-1}^{1} f(x) dx
\end{align}

となる．

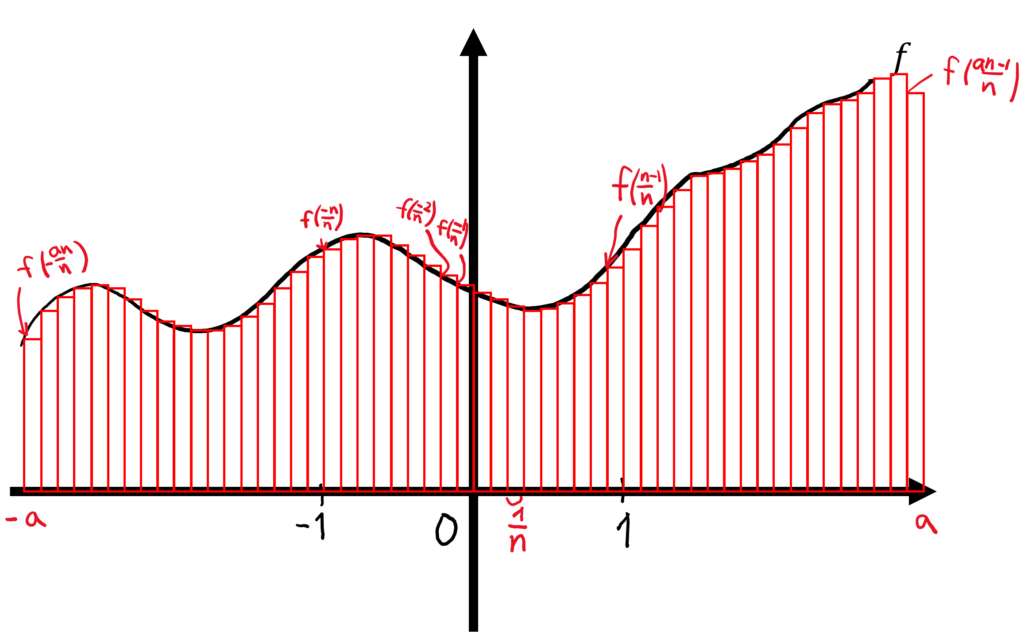
積分範囲が区間\([-a,a]\)のとき和の範囲はどのようになるだろうか．この場合も関数\(f\)の引数に注意すると総和\(\sum\)の範囲が変化し，

\begin{align}
\lim_{n \to \infty} \sum_{k=-an}^{an-1}f\left( \frac{k}{n} \right) \frac{1}{n} &= \int_{-a}^{a} f(x) dx
\end{align}

となる．

そして，\(a \to \infty\)を考えると

\begin{align}
\lim_{n \to \infty}\lim_{a \to \infty} \sum_{k=-an}^{an-1}f\left( \frac{k}{n} \right) \frac{1}{n} &= \int_{-\infty}^{\infty} f(x) dx\\
\lim_{n \to \infty} \sum_{k=-\infty}^{\infty}f\left( \frac{k}{n} \right) \frac{1}{n} &= \int_{-\infty}^{\infty} f(x) dx
\end{align}

区分求積法では

\begin{align}
\lim_{n \to \infty} \sum_{k=-\infty}^{\infty}g\left( \frac{k}{n} \right) \frac{1}{n} &= \int_{-\infty}^{\infty} g(\omega) d\omega
\end{align}

ただし，

\begin{align}
\omega
&= \lim_{\Delta \omega \to 0} k\Delta \omega\\
&= \lim_{T \to \infty}\omega_k \\
&= \lim_{T \to \infty} \frac{2\pi}{T}k \\
&= \lim_{n \to \infty} \frac{k}{n}
\end{align}

また，

\begin{align}
d\omega
&= \lim_{\Delta \omega \to 0} \Delta \omega\\
&= \lim_{T \to \infty} \frac{2\pi}{T} \\
&= \lim_{n \to \infty} \frac{1}{n}
\end{align}

なので\(x(t)\)は

\begin{align}
x(t)
&= \lim_{n \to \infty} \sum_{k=-\infty}^{\infty} g\left (\frac{k}{n} \right ) \frac{1}{n}\\
&= \int_{-\infty}^{\infty} g(\omega) d\omega \\
&= \int_{-\infty}^{\infty} \left( \frac{1}{2\pi}\int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt\right) e^{j\omega t} d\omega \\
\end{align}

ここで\(X(\omega) = \frac{1}{2\pi}\int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt\)とおくと

\begin{align}
x(t) &= \int_{-\infty}^{\infty} F(\omega) e^{j\omega t} d\omega \\
\end{align}

このとき\(X(\omega)= \frac{1}{2\pi}\int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt\)を関数\(x(t)\)のフーリエ変換とよぶ．

また\(x(t) = \int_{-\infty}^{\infty} X(\omega) e^{j\omega t} d\omega\)をフーリエ逆変換と呼ぶ．

寄り道：フーリエ逆変換と逆フーリエ変換

フーリエ逆変換と逆フーリエ変換はどちらも同じくフーリエ変換の逆変換を指しているが，どちらを採用するかは書籍によって異なる．

どちらか一方を採用するとしたらどちらだろうか…

手元の書籍でどちらを採用しているか調べてみると，以下のようにフーリエ逆変換が多かった．変換と逆変換の対を意識しているのだろうか．

フーリエ逆変換 4冊
8834464 1 apa 50 default 1363

大石進一. (1989). フーリエ解析. 岩波書店.

クライツィグ E., & Kreyszig, E. (2003). フーリエ解析と偏微分方程式 (近藤次郎, 阿部寛治, & 堀素夫, Trans.; 第8版). 培風館.

船越満明. (1997). キーポイントフーリエ解析. 岩波書店.

畑上到. (2014). 工学基礎フーリエ解析とその応用[新訂版]: 0 (新訂版). 数理工学社.
フーリエ変換の逆変換(反転公式) 2冊
8834464 {8834464:YLD6AW99},{8834464:JT4VDEYH} 1 apa 50 default 1363

洲之内源一郎. (1977). フーリエ解析とその応用. サイエンス社.

今村勤. (1976). 物理とフーリエ変換. 岩波書店.
逆フーリエ変換 1冊
8834464 {8834464:BF8FGIMH} 1 apa 50 default 1363

M.R.スピーゲル. (1982). ラプラス変換 (土井誠, Trans.). マグロウヒル出版.