今回の目的
確率過程について理解する.
確率過程(Stochastic process)とは…
時間とともに変化する確率変数\(\{x(t), t \in T\}\)である.別の言い方をすれば各時刻ごとの値の列を生み出すような確率的な構造を確率過程と呼ぶ.
例:株価,為替,ブラウン運動
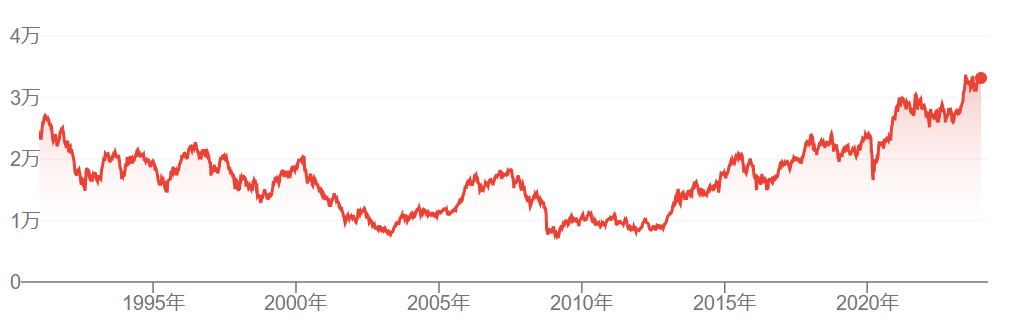 日経平均の時系列(Google Financeから引用)
日経平均の時系列(Google Financeから引用)
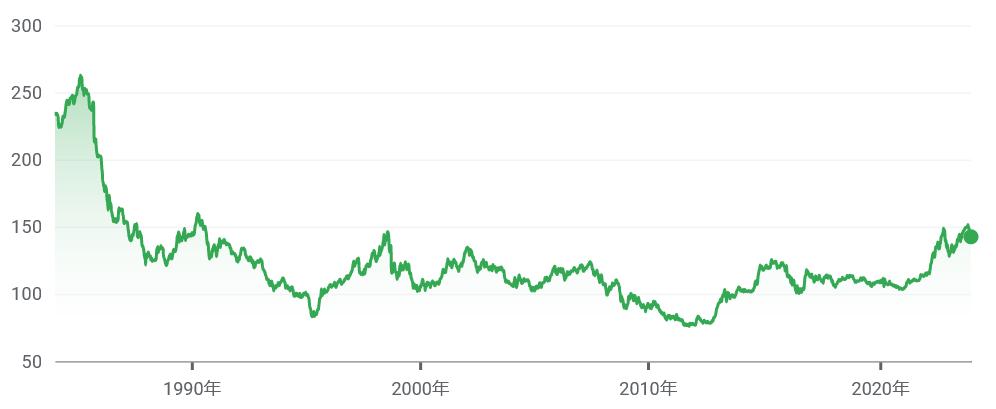 ドル円の為替レートの時系列(Google Financeから引用)
ドル円の為替レートの時系列(Google Financeから引用)
株価の推移といった時系列は基本的に1本の有限な時系列しか得られない.その時系列を確率的な構造によって生み出されうる多くの可能な時系列の一つに過ぎないとみなし,その背後にある構造を明らかにすることが時系列の解析の目的である.
定常性(弱定常)
確率過程が定常であるということは"統計的性質が時間とともに変化しない"ということである.
最も強い定常性は各時刻の確率変数が従う確率分布が時間に関して不変であることだが,それを少し緩めた概念としてm次のモーメント\(E[X^m]\)までを同等とした\(m\)次定常が良く用いられる.
特に2次定常は
・\(E[X]=\mu\)が時間に関して不変
・\(E[X^2]\)が時間に関して不変
となる確率過程であり,弱定常とも呼ばれる.
弱定常な確率過程では一つの実現された時系列から推定される1次と2次のモーメントは時間が長くなるほど真の値へと近づいていく.
自己共分散関数と自己相関関数
\(X_t\)を2次定常な確率過程としたとき,\(X_t\)と\(X_{t+\tau}\)の自己共分散関数\(R_{xx}(\tau)\)は以下のように定義される.
\begin{align}
R_{xx}(\tau) &= E[(X_t-\mu)(X_{t+\tau}-\mu)]
\end{align}
自己相関関数は\(\tau\)ステップ先と現在の確率変数の関係を表しており,確率過程を特徴づける重要な量である.
また,分散\(\sigma^2 = R_{xx}(0)\)によって規格化した自己共分散関数を自己相関関数\(\rho_{xx}(\tau)\)と呼ぶ.
\begin{align}
\rho_{xx}(\tau) &= \frac{R_{xx}(\tau)}{R_{xx}(0)}
\end{align}
相互共分散関数と相互相関関数
2変量の定常確率過程を考えるときには自己共分散関数だけでなく相互共分散関数に確率変数間の関係を調べることができる.
\(X_t,Y_t\)を2次定常な確率過程としたとき,\(X_t\)と\(Y_{t+\tau}\)の自己共分散関数\(R_{xx}(\tau)\)は以下のように定義される.
\begin{align}
R_{xy}(\tau) &= E[(X_t-\mu_x)(Y_{t+\tau}-\mu_y)]
\end{align}
また,それぞれの標準偏差\(\sigma_x=\sqrt{R_{xx}(0)}, \sigma_y=\sqrt{R_{yy}(0)}\)によって規格化した相互共分散関数を相互相関関数\(\rho_{xy}(\tau)\)と呼ぶ.
\begin{align}
\rho_{xy}(\tau) &= \frac{R_{xy}(\tau)}{\sqrt{R_{xx}(0)R_{yy}(0)}}
\end{align}
参考文献
8834464
{8834464:BZN27AR7}
apa
50
2044
https://nakamura.sciotein.com/wp-content/plugins/zotpress/
%7B%22status%22%3A%22success%22%2C%22updateneeded%22%3Afalse%2C%22instance%22%3A%22zotpress-48f2fddd422d293a1831e8d35354176a%22%2C%22meta%22%3A%7B%22request_last%22%3A0%2C%22request_next%22%3A0%2C%22used_cache%22%3Atrue%7D%2C%22data%22%3A%5B%7B%22key%22%3A%22BZN27AR7%22%2C%22library%22%3A%7B%22id%22%3A8834464%7D%2C%22meta%22%3A%7B%22creatorSummary%22%3A%22%5Cu5c3e%5Cu5d0e%22%2C%22parsedDate%22%3A%221989-01-01%22%2C%22numChildren%22%3A1%7D%2C%22bib%22%3A%22%3Cdiv%20class%3D%5C%22csl-bib-body%5C%22%20style%3D%5C%22line-height%3A%202%3B%20padding-left%3A%201em%3B%20text-indent%3A-1em%3B%5C%22%3E%5Cn%20%20%3Cdiv%20class%3D%5C%22csl-entry%5C%22%3E%26%23x5C3E%3B%26%23x5D0E%3B%26%23x7D71%3B.%20%281989%29.%20%3Ci%3E%26%23x6642%3B%26%23x7CFB%3B%26%23x5217%3B%26%23x8AD6%3B%3C%5C%2Fi%3E.%20NHK%26%23x51FA%3B%26%23x7248%3B.%3C%5C%2Fdiv%3E%5Cn%3C%5C%2Fdiv%3E%22%2C%22data%22%3A%7B%22itemType%22%3A%22book%22%2C%22title%22%3A%22%5Cu6642%5Cu7cfb%5Cu5217%5Cu8ad6%22%2C%22creators%22%3A%5B%7B%22creatorType%22%3A%22author%22%2C%22firstName%22%3A%22%5Cu7d71%22%2C%22lastName%22%3A%22%5Cu5c3e%5Cu5d0e%22%7D%5D%2C%22abstractNote%22%3A%22%22%2C%22date%22%3A%221989-01-01%22%2C%22language%22%3A%22%5Cu65e5%5Cu672c%5Cu8a9e%22%2C%22ISBN%22%3A%22978-4-14-564341-4%22%2C%22url%22%3A%22%22%2C%22collections%22%3A%5B%5D%2C%22dateModified%22%3A%222024-01-04T01%3A23%3A15Z%22%7D%7D%5D%7D
尾崎統. (1989). 時系列論. NHK出版.




ディスカッション
コメント一覧
まだ、コメントがありません