生物工学演習D -第2回- 機械力学系における微分方程式モデル
今回の目標
□機械力学系の運動方程式を立てることができるようになる.
□機械力学系の微分方程式モデル(運動方程式)の解をラプラス変換を用いて求めることができるようになる.
機械力学系とは(Mechanical Systems)
機械力学系は物体がどのように動くのか,またどのような力が働いているのかを調べる学問である.
日常生活に見られる機械力学系の例に車のサスペンションがある.サスペンションの主要な部品にはバネやダンパが存在し,路面から車体に加わる衝撃を吸収し乗り心地を向上させる.例えばサスペンションを微分方程式でモデル化し,解を調べることで適切なばね定数や,ダンパの粘性を選択できる.
運動方程式の立式とラプラス変換を用いた解法
機械力学系の支配方程式の基本はニュートンの運動の第2法則である.
\begin{align}
m\frac{d^2x(t)}{dt^2}=f(t)
\end{align}
この微分方程式の力\(f\)を状況に応じて具体的に代入することで運動方程式を立式できる.
運動方程式が立式し,初期条件が決まれば第一回の手法でその機械力学系の解を求めることができる.
例1:空気の粘性抵抗を受ける台車の運動
以下のように抵抗率\(b\)で速度に比例する抵抗を受けながら移動する台車を考える.

ここで入力は力\(u(t)\),出力は台車の変位\(x(t)\)とする.
また簡単のため初期条件として\(x(0) = 0\),\(\frac{d}{dt}x(t)|_{t=0} = 0\)とする.
練習のため入力\(u(t)\)としてインパルス入力とステップ入力の2種類を考える.
運動方程式の立式
このとき運動方程式は
\begin{align}
m\frac{d^2}{dt^2}x(t)&=f(t)\\
m\frac{d^2}{dt^2}x(t)&=u(t) – b\frac{d}{dt}x(t)
\end{align}
ラプラス変換による解の導出
ラプラス変換すると
\begin{align}
m(s^2X(s)-sx(0)-\frac{d}{dt}x(t)|_{t=0})&=U(s) – b(sX(s)-x(0))\\
m(s^2X(s)-0-0)&=U(s) – b(sX(s)-0)\\
ms^2X(s)&=U(s) – bsX(s)\\
(ms^2+bs)X(s)&=U(s)\\
X(s)&=\frac{1}{(ms^2+bs)}U(s)
\end{align}
以下で2種類の具体的な入力\(u(t)\)について考える.
インパルス入力の場合
\begin{align}
u(t) = \delta (t) \text{:ディラックのデルタ関数}
\end{align}
このとき\(U(s) = 1\).
よって
\begin{align}
X(s)&=\frac{1}{(ms^2+bs)}U(s) \\
X(s)&=\frac{1}{(ms^2+bs)} \\
X(s)&=\frac{1}{b}\frac{1}{s} – \frac{m}{b}\frac{1}{ms + b}\\
X(s)&=\frac{1}{b}\frac{1}{s} – \frac{1}{b}\frac{1}{s + \frac{b}{m}}
\end{align}
両辺を逆ラプラス変換すると
\begin{align}
x(t)&=\frac{1}{b} – \frac{1}{b}e^{-\frac{b}{m}}
\end{align}
初めの一瞬押した力で台車は前方へと進むが空気抵抗により\(\frac{1}{b}\)進んだところで止まることが式からわかる.
ステップ入力の場合
\begin{align}
u(t) = \left\{
\begin{array}{ll}
0 & \mathrm{for}\ t < 0 \\
1 & \mathrm{for}\ t \ge 0
\end{array}
\right.
\end{align}
このとき\(U(s) = \frac{1}{s}\).
よって
\begin{align}
X(s)&=\frac{1}{(ms^2+bs)}U(s) \\
X(s)&=\frac{1}{(ms^2+bs)}\frac{1}{s} \\
X(s)&=\frac{1}{s^2(ms+b)} \\
X(s)&=\frac{c_1}{s} + \frac{c_2}{s^2} + \frac{c_3}{(ms+b)}
\end{align}
右辺の部分分数分解前後に\(s^2(ms+b)\)をかけると
\begin{align}
1&=c_1 s(ms+b) + c_2(ms+b) + c_3 s^2\\
1&=(m c_1 + c_3)s^2 + (b c_1 + m c_2) s + b c_2
\end{align}
係数を比較すると,\(c_2 = \frac{1}{b}, c_1 = -\frac{m}{b^2}, c_3 = \frac{m^2}{b^2}\)
\begin{align}
X(s)&=-\frac{m}{b^2}\frac{1}{s} + \frac{1}{b}\frac{1}{s^2} + \frac{m^2}{b^2}\frac{1}{(ms+b)}\\
X(s)&=-\frac{m}{b^2}\frac{1}{s} + \frac{1}{b}\frac{1}{s^2} + \frac{m}{b^2}\frac{1}{(s+\frac{b}{m})}
\end{align}
両辺を逆ラプラス変換すると
\begin{align}
x(t)&=-\frac{m}{b^2} + \frac{1}{b}t + \frac{m}{b^2}e^{-\frac{b}{m}t}
\end{align}
例2:倒立単振子モデル
回転運動の場合には以下のような微分方程式を考える.
\begin{align}
I\frac{d^2}{dt^2}\theta (t)&=\tau (t)
\end{align}
倒立振子の微分方程式は
\begin{align}
I\frac{d^2}{dt^2}\theta (t) &=mgh \sin\theta – k\theta (t) – b\frac{d}{dt} \theta (t) + \tau_\mathrm{input}(t)
\end{align}
質量が原点から\(h\)の高さの点に集中している質点の場合,慣性モーメントは\(I=mh^2\)となる.
また,角度\(\theta\)が十分に小さいとき\(\sin \theta \approx \theta\)となる.
そのため角度が小さいときには上記の微分方程式を以下のように線形化することができる.
\begin{align}
mh^2\frac{d^2}{dt^2}\theta (t) &=mgh \theta (t) – k\theta (t) – b\frac{d}{dt} \theta (t) + \tau_\mathrm{input}(t)\\
mh^2\frac{d^2}{dt^2}\theta (t) &=(mgh-k) \theta (t) – b\frac{d}{dt} \theta (t) + \tau_\mathrm{input}(t)\\
\end{align}
この両辺をラプラス変換すると
\begin{align}
mh^2(s^2\Theta(s)-s\theta(0)-\frac{d}{dt}\theta(t)|_{t=0}) &=(mgh-k) \Theta (s) – b(s\Theta(s)-\theta(0)) + T_\mathrm{input}(s)\\
mh^2(s^2\Theta(s)-0-0) &=(mgh-k) \Theta (s) – b(s\Theta(s)-0)+ T_\mathrm{input}(s)\\
mh^2 s^2\Theta(s) &=(mgh-k) \Theta (s) – bs\Theta(s)+ T_\mathrm{input}(s)\\
(mh^2 s^2 + bs + k – mgh)\Theta(s) &= T_\mathrm{input}(s)\\
\Theta(s) &= \frac{1}{mh^2 s^2 + bs + (k – mgh)} T_\mathrm{input}(s)\\
\end{align}
インパルス応答を考えると\(T_\mathrm{input}(s) = 1\),
さらにラプラス変換対応表の形に変形すると(詳細は略)
\begin{align}
\Theta(s) &= \frac{1}{mh^2 s^2 + bs + (k – mgh)}\\
\Theta(s) &= \frac{1}{mh^2}\frac{1}{(s+\alpha)^2 + \beta^2}
\end{align}
と変形できる.\(\alpha\)と\(\beta\)は平方完成で計算してください.
これを逆ラプラス変換すると
\begin{align}
\theta(t) &= \frac{1}{mh^2}e^{-\alpha t}\frac{1}{\beta}\sin(\beta t) \\
\end{align}
参考:ラプラス変換対応表
| \(f(t)\) | \(F(s)\) |
| \(1\) | \(\frac{1}{s}\) |
| \(t\) | \(\frac{1}{s^2}\) |
| \(t^n\) | \(\frac{n!}{s^{n+1}}\) |
| \(e^{at}\) | \(\frac{1}{s-a}\) |
| \(\delta(t)\) | \(1\) |
| \(\sin(\omega t)\) | \(\frac{\omega}{s^2+\omega^2}\) |
| \(\cos(\omega t)\) | \(\frac{s}{s^2+\omega^2}\) |
| \(f(t)\) | \(F(s)\) |
| \(\frac{d}{dt}f(t)\) | \(sF(s)-f(0)\) |
| \(\frac{d^2}{dt^2}f(t)\) | \(s^2F(s)-sf(0)-\frac{d}{dt}f(t)|_{t=0}\) |
| \(\int_0^t f(t) dt\) | \(\frac{1}{s} F(s)\) |
| \(e^{at}f(t)\) | \(F(s-a)\) |
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p63-
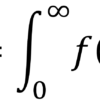


ディスカッション
コメント一覧
まだ、コメントがありません