生物工学演習D -第3回- ブロック線図 システム構造の視覚的表現
今回の目標
□ブロック線図とシステムの微分方程式モデルの関係を理解する
□ブロック線図の等価交換ができるようになる
ブロック線図とは(Block Diagrams)
ブロック線図は,システム制御工学において,システムやプロセスの構成要素とそれらの相互作用を視覚的に表現するために使用されるグラフィカルな表現方法.ブロック線図は,制御システムの設計,解析,評価において非常に役立つツールであり,システムの動作や性能を理解しやすくするために用いられる.
chatGPT
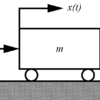
以下の図のような例がわかりやすい.ブロック線図ではシステムの各要素をブロックとして表し,その入出力関係を矢印で表現することができる.
さらに下記で紹介するブロック線図の等価交換により,システム全体の入出力関係についても考えることができる.
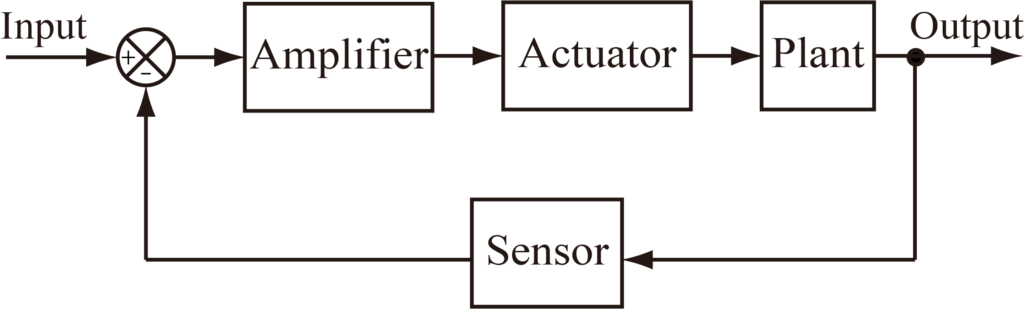
ブロック線図の構成要素
ブロック線図としては時間領域のブロック線図と周波数領域(ラプラス変換後)のブロック線図があるが本講義では周波数領域のブロック線図のみ扱う.
ブロック
一つの入力と出力の関係を示す.下図は例.
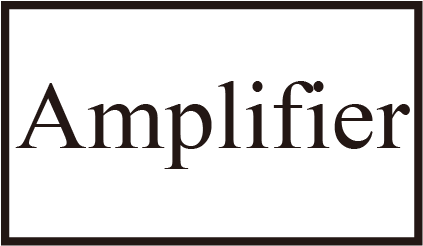
矢印
信号の流れる向きを表し,各ブロックの入力と出力の流れを示す.

和差器
複数の信号の和,もしくは差をとる.各矢印の先の符号によって和か差が決まる.
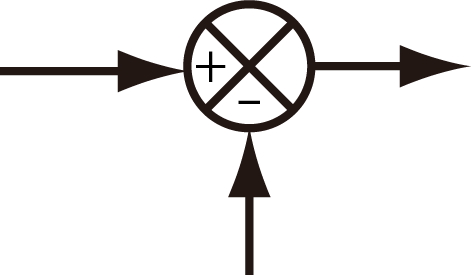
分岐点(引き出し点)
一つの信号を複数に分岐させるときは黒点で表す.基本的に点がない場合は交差していても線はつながっていないとみなす.

ブロック線図の等価交換
ブロック線図は入出力関係を表すが,二つのブロックの入力と出力を一つのブロックとみなして等価なブロック線図を書くことができる.
直列
以下のような直列につながった二つのブロックを考える.
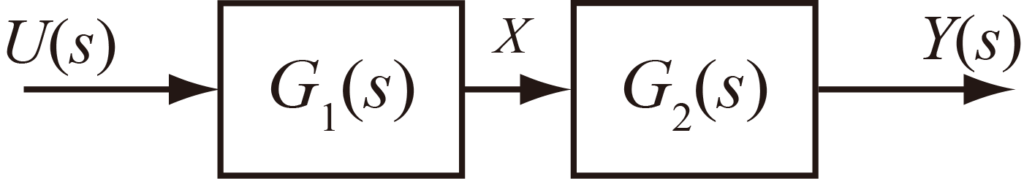
この二つのブロックの間の矢印上の信号を\(X(s)\)とすると,
\begin{align}
Y(s) &= G_2(s) X(s)\\
X(s) &= G_1(s) U(s)
\end{align}
と書けるので\(X(s)\)を消すと,
\begin{align}
Y(s) &= G_2(s) G_1(s) U(s)
\end{align}
となる.
よって直列につながった二つのブロック線図は以下のブロック線図に変換できる.
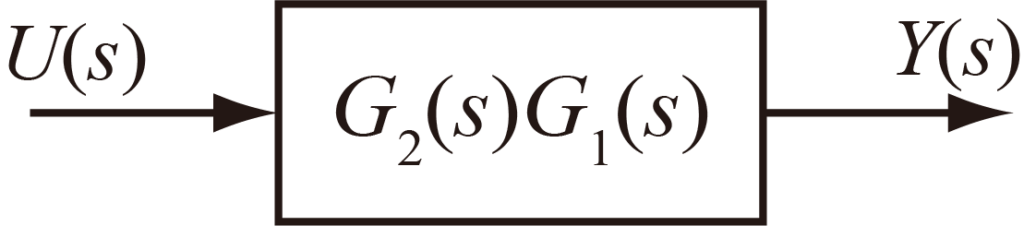
並列
以下のような並列につながった二つのブロックを考える.
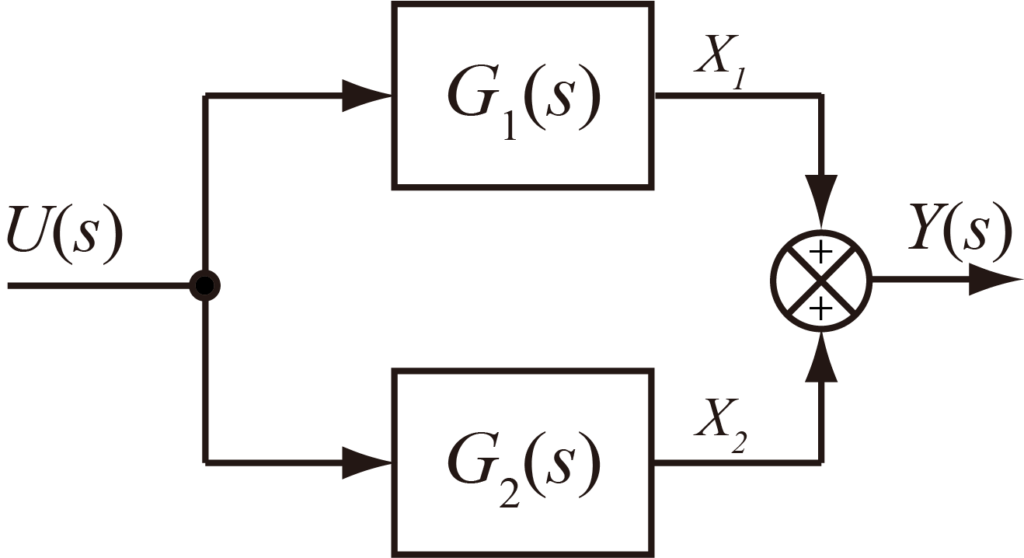
この二つのブロックの出力信号をそれぞれ\(X_1(s)\),\(X_2(s)\)とすると,
\begin{align}
X_1(s) &= G_1(s) U(s)\\
X_2(s) &= G_2(s) U(s)\\
Y(s) &= X_1(s) + X_2(s)
\end{align}
と書けるので\(X_1(s)\),\(X_2(s)\)を消すと,
\begin{align}
Y(s) &= G_1(s) U(s) + G_2(s) U(s)\\
Y(s) &= (G_1(s) + G_2(s)) U(s)
\end{align}
となる.
よって直列につながった二つのブロック線図は以下のブロック線図に変換できる.
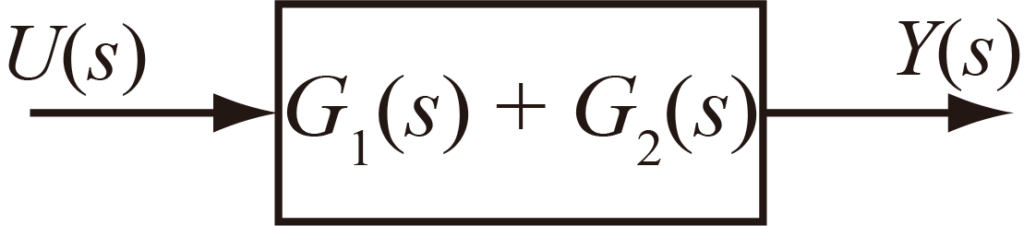
フィードバック
以下のようなフィードバックのある矢印でつながった二つのブロックを考える.
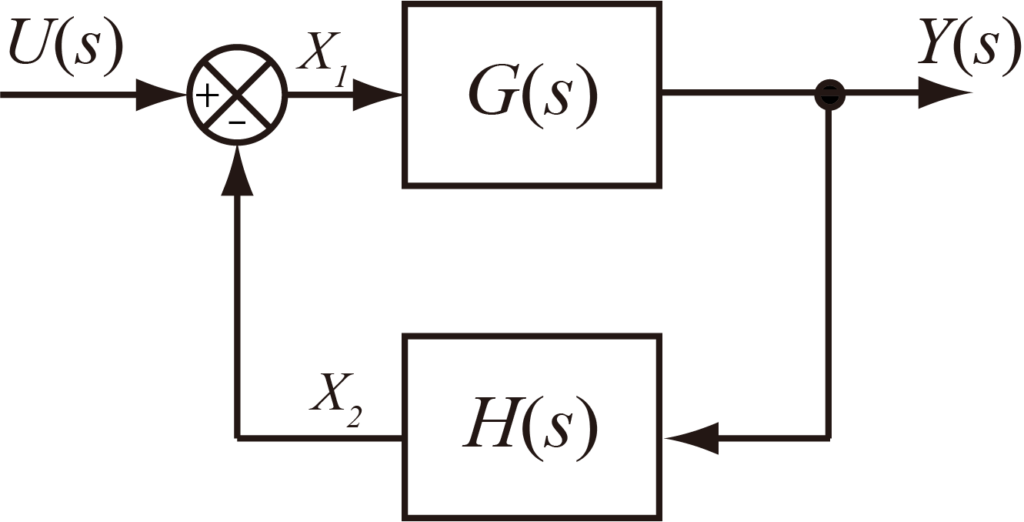
この和差器の出力とフィードバックブロックの出力の信号をそれぞれ\(X_1(s)\),\(X_2(s)\)とすると,
\begin{align}
X_1(s) &= U(s) – X_2(s)\\
X_2(s) &= H(s) Y(s)\\
Y(s) &= G(s) X_1(s)
\end{align}
と書けるので\(X_1(s)\),\(X_2(s)\)を消すと,
\begin{align}
Y(s) &= G(s) (U(s) – X_2(s))\\
Y(s) &= G(s) (U(s) – H(s) Y(s))\\
(1+G(s)H(s))Y(s) &= G(s) U(s)\\
Y(s) &= \frac{G(s)}{1+G(s)H(s)} U(s)\\
\end{align}
となる.
よって直列につながった二つのブロック線図は以下のブロック線図に変換できる.

参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p17-p29
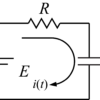



ディスカッション
コメント一覧
まだ、コメントがありません