生物工学演習D -第10回- システムの状態空間表現
今回の目標
□状態空間表現でシステムを表現する方法を理解する
□状態遷移行列を計算する方法を理解する
システムの状態空間表現

例として上記の図のようにバネにつながった抵抗率bで速度に比例する抵抗を受けながら移動する台車を考える.
このとき運動方程式は
\begin{align}
m\frac{d^2}{dt^2}x(t)&= -kx(t) – b\frac{d}{dt}x(t) + u(t)
\end{align}
となる.
このとき,状態変数として\(x_1(t) = x(t), x_2(t) = \frac{d}{dt}x(t)\)とおくと上記の運動方程式は
\begin{align}
\frac{d}{dt}x_1(t)&=x_2(t)\\
\frac{d}{dt}x_2(t)&= -\frac{k}{m}x_1(t) – \frac{b}{m}x_2(t) + \frac{1}{m} u(t)
\end{align}
状態変数を縦ベクトル\(\boldsymbol{x} = (x_1(t) \ x_2(t))^T\)と行列で表現すると
\begin{align}
\frac{d}{dt}
\begin{pmatrix}
x_1(t) \\
x_2(t) \\
\end{pmatrix}
&=
\begin{pmatrix}
0 & 1 \\
-\frac{k}{m} & – \frac{b}{m}\\
\end{pmatrix}
\begin{pmatrix}
x_1(t) \\
x_2(t) \\
\end{pmatrix}
+
\begin{pmatrix}
0 \\
\frac{1}{m} \\
\end{pmatrix}
u(t)
\end{align}
ここで
\begin{align}
A &=
\begin{pmatrix}
0 & 1 \\
-\frac{k}{m} & – \frac{b}{m}\\
\end{pmatrix}
\\
B &=
\begin{pmatrix}
0 \\
\frac{1}{m} \\
\end{pmatrix}
\end{align}
とおくと
\begin{align}
\frac{d}{dt}
\boldsymbol{x}
&=
A\boldsymbol{x}
+
Bu(t)
\end{align}
が得られる.この式は状態方程式と呼ばれる.
また,システムの出力\(y\)を台車の位置\(x_1(t)\)とすると
\begin{align}
y
&=
\begin{pmatrix}
1 & 0
\end{pmatrix}
\begin{pmatrix}
x_1(t) \\
x_2(t) \\
\end{pmatrix}\\
&=C \boldsymbol{x}
\end{align}
この式は出力方程式と呼ばれる.
状態方程式と出力方程式の2つを合わせてシステムの状態空間表現と呼ぶ.
注意点:あるシステムの状態空間表現は一意ではなく状態変数の選び方によってさまざまな表現がある.
状態空間表現における状態の時間発展と状態遷移行列
上記のような状態空間表現が得られたときその時間発展は以下のように書ける.
\begin{align}
\boldsymbol{x}(t)
&=
e^{At}\boldsymbol{x}(0)
+
\int_0^t e^{A(t-\tau)}Bu(\tau) d\tau
\end{align}
状態方程式を変形すると
\begin{align}
\frac{d}{dt}
\boldsymbol{x}
&=
A\boldsymbol{x}
+
Bu(t)\\
\frac{d}{dt}
\boldsymbol{x}
–
A\boldsymbol{x}
&=
Bu(t)\\
\end{align}
両辺に\(e^{-At}\)をかけると
\begin{align}
e^{-At}(
\frac{d}{dt}
\boldsymbol{x}
–
A\boldsymbol{x})
&=
e^{-At}Bu(t)\\
\frac{d}{dt}(e^{-At}\boldsymbol{x})
&=
e^{-At}Bu(t)\\
\end{align}
両辺を積分すると
\begin{align}
\int_0^t \frac{d}{d\tau}(e^{-A\tau} \boldsymbol{x}) d\tau
&=
\int_0^t e^{-A\tau}Bu(\tau) d\tau\\
[e^{-A\tau} \boldsymbol{x}(\tau)]_{\tau=0}^t
&=
\int_0^t e^{-A\tau}Bu(\tau) d\tau\\
e^{-At} \boldsymbol{x}(t) – e^{-A0} \boldsymbol{x}(0)
&=
\int_0^t e^{-A\tau}Bu(\tau) d\tau\\
e^{-At} \boldsymbol{x}(t)
&=
\boldsymbol{x}(0) + \int_0^t e^{-A\tau}Bu(\tau) d\tau\\
\boldsymbol{x}(t)
&=
e^{At}\boldsymbol{x}(0) + e^{At}\int_0^t e^{-A\tau}Bu(\tau) d\tau\\
\boldsymbol{x}(t)
&=
e^{At}\boldsymbol{x}(0) + \int_0^t e^{-A(\tau-t)}Bu(\tau) d\tau\\
\end{align}
状態遷移行列\(e^{At}\)の計算法
入力\(u(t)=0\)の同次形を考える.
\begin{align}
\frac{d}{dt}
\boldsymbol{x}
&=
A\boldsymbol{x}
\end{align}
両辺をラプラス変換すると
\begin{align}
s\boldsymbol{X}(s) – \boldsymbol{x}(0) &= A\boldsymbol{X}(s)\\
(sI – A)\boldsymbol{X}(s) &= \boldsymbol{x}(0)\\
\boldsymbol{X}(s) &= (sI – A)^{-1}\boldsymbol{x}(0)\\
\boldsymbol{x}(t) &= L^{-1}[(sI – A)^{-1}]\boldsymbol{x}(0)\\
\end{align}
このとき解は
\begin{align}
\boldsymbol{x}(t)
&=
e^{At}\boldsymbol{x}(0)
\end{align}
つまり状態遷移行列は\(\Phi(t)\)
\begin{align}
\Phi(t) = e^{At} = L^{-1}[(sI – A)^{-1}]
\end{align}
参考文献
[0] Ogata, Katsuhiko. Modern Control Engineering. 5th ed. Prentice-Hall Electrical Engineering Series. Instrumentation and Controls Series. Boston: Prentice-Hall, 2010. p649-
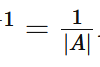

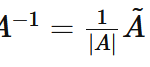

ディスカッション
コメント一覧
まだ、コメントがありません