生物工学演習E -第5回- 信号のサンプリング どれほど細かくサンプリングすべきか?
今回の概要
信号のサンプリングにより,連続時間信号から離散時間信号に変換される.
サンプリング周波数が信号がもつ最大周波数の倍のとき,離散信号から連続信号を復元できる.
信号のサンプリング:時間の離散化
生体信号などの計測を行う際,実世界での連続時間信号をサンプリングし,離散時間信号としてPCなどに記録する.
今回はサンプリングの間隔によって,得られる離散信号の性質がどのように変化するかを考える.
連続信号\(x(\cdot)\)をサンプリング間隔\(T_s\)でサンプリングすると以下のような離散信号\(\boldsymbol{x} = \{x_k \}\)が得られる.
\begin{align}
x_k = x(kT_s)
\end{align}
このとき,\(f_s = \frac{1}{T_s}\)をサンプリング周波数とよぶ.また,\(\omega_s = 2\pi f_s\)をサンプリング角周波数とよぶ.
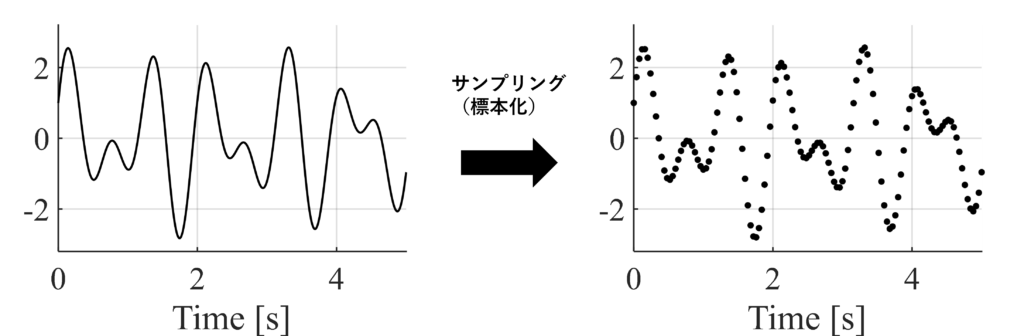
サンプリング(sampling)は定義域の離散化
サンプリングは上記で示したように時間を離散化して連続時間信号を離散時間信号に変換すること.
時間:離散,信号の値:連続

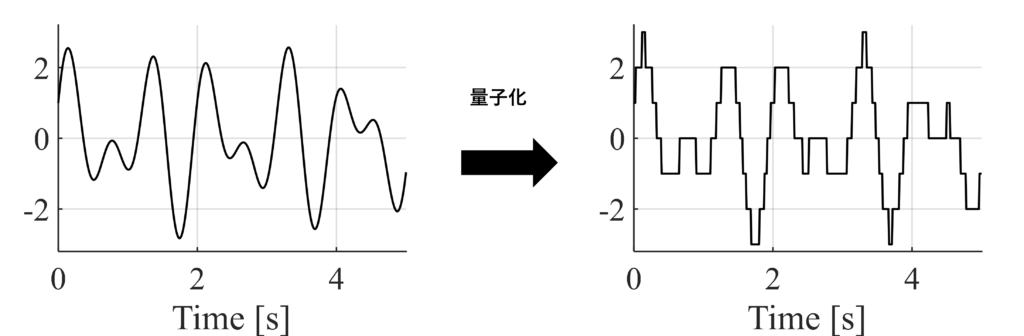
量子化(quantizing)は値域の離散化
量子化は連続的な値をとる信号を,加算個の値で近似して離散化すること.
時間:連続,信号の値:離散
正規化角周波数:1サンプル時間で進む位相
サンプリングによって"正規化された"離散時間信号\(\boldsymbol{x}=\{x_0,x_1,x_2,\dots\}\)を取り扱う時は角周波数も正規化すると,サンプリング間隔に依存せず信号の解析を行うことができる.
このような角周波数を正規化角周波数とよび,ここでは\(\tilde{\omega}\)で表す.
\(\tilde{\omega} = \omega T_s = 2\pi f T_s\)
正規化角周波数\(\tilde{\omega}\)は1サンプルを取得する間に位相が何ラジアン進むのかを表している.
例えば
\begin{align}
\tilde{\omega} = \frac{\pi}{2}
\end{align}
のとき,1サンプルごとに位相は\(\frac{\pi}{2}\)進み,4サンプルで\(\frac{\pi}{2}\times4 = 2\pi\)と1周する.
折り返し雑音:\(\tilde{\omega}\)と\(\tilde{\omega}+2\pi\)の波を区別できない
サンプリングによる信号の離散化によって,連続時間信号では見られなかった性質が現れる.
その一つが\(\tilde{\omega}\)と\(\tilde{\omega}+2\pi\)の正規化各周波数を持つ波(三角関数や複素指数関数)が同じ関数になってしまうという性質である.
例えば
\begin{align}
\cos((\tilde{\omega}+2\pi)k) &= \cos(\tilde{\omega}k+2\pi k)\\
&= \cos(\tilde{\omega}k)\cos(2\pi k) – \sin(\tilde{\omega}k)\sin(2\pi k)\\
\end{align}
ここで\(k\in\{0,1,2,\dots\}\)より\(2\pi k\)は常に\(2\pi\)の倍数なので\(\cos(2\pi k) =1\),\(\sin(2\pi k) =0\).
よって
\begin{align}
\cos((\tilde{\omega}+2\pi)k)
&= \cos(\tilde{\omega}k)\times 1 – \sin(\tilde{\omega}k)\times 0\\
&= \cos(\tilde{\omega}k)
\end{align}
となり\(\tilde{\omega}\)と\(\tilde{\omega}+2\pi\)の正規化角周波数を持つ波を区別できないことがわかる.
つまり,元の信号にこれらの波が含まれていた場合,サンプリングによってこれらの波は同じ正規化角周波数になってしまい情報が失われてしまう.
例えば以下の例では信号は\(x(t) = \cos(2\pi t)\)を黒破線でプロットしている.この信号を2 Hz, つまりサンプリング間隔 0.5 s でサンプリングしたとき,黒丸のようなデータが得られる.
一方上記の話では正規化角周波数\(\tilde{\omega}\)に\(2\pi\)を足した信号も同じ離散信号になるのだった.
正規化角周波数は\(\tilde{\omega} = \omega T_s\)より角周波数は\( \omega = \frac{\tilde{\omega}}{T_s}\).
つまり,サンプリング間隔\(T_s = 0.5\)のとき,正規化角周波数で\(2\pi\)を足すことは,元の角周波数において\(\frac{2\pi}{T_s} = 2\pi / 0.5 = 4\pi \)の角周波数を足した連続信号を考えることに相当する.
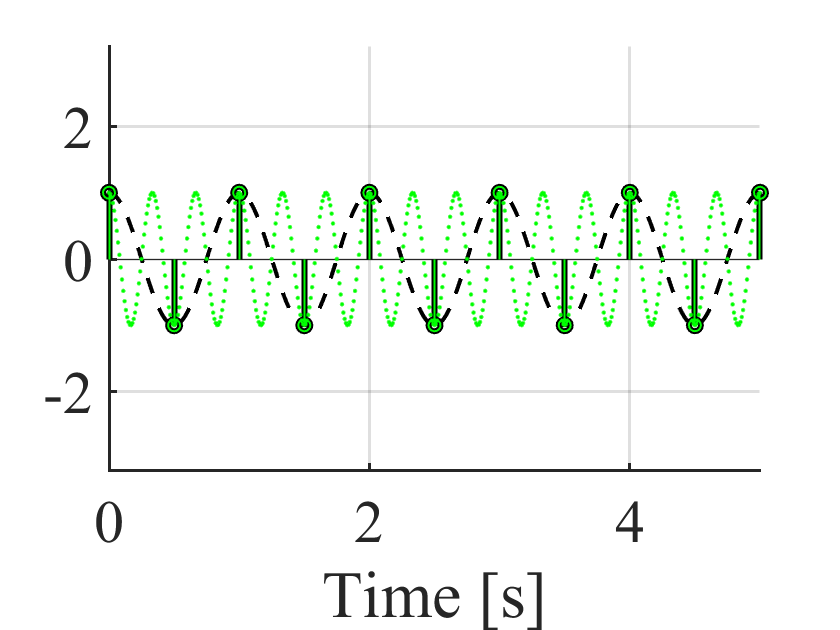
図は例として角周波数\(2\pi\times 1\) (周波数1 Hz)の信号と角周波数\(2\pi + 4\pi = 2\pi \times 3\)(3 Hz)の信号をプロットして,0.5 s間隔でサンプリングしたものである.
図からわかるように離散化後,2つの信号を区別することができない.
同じことは\(2\pi \times n\), (\(n\)は整数)の正規化角周波数を加えた場合にも成り立つ.
一応,連続信号の場合を復習すると
\begin{align}
\cos((\omega+2\pi)t) &= \cos(\omega t+2\pi t)\\
&= \cos(\omega t)\cos(2\pi t) – \sin(\omega t)\sin(2\pi t)
\end{align}
となるが,tは連続値のため\(\cos(2\pi t) \)や\(\sin(2\pi t)\)は\(t\)の値に依存して様々な値をとる.
つまり連続時間信号における三角関数や複素指数関数が表す波は各周波数に\(2\pi\)を足したものと区別できる.
\(\tilde{\omega}\)と\(2\pi – \tilde{\omega}\)の波も区別できない
先ほどは正規化角周波数(\tilde{\omega})に\(2\pi\)足した時の波を区別できないという話だった.
次に気になるのは正規化角周波数が\(2\pi\)増えるまでの間はサンプリングをしても同じ周波数になることはないのだろうか.
実は,正規化角周波数が\(2\pi\)増加するまでの間でも同じ周波数になってしまう周波数が存在する.
それは正規化角周波数が\(2\pi – \tilde{\omega}\)のときである.
\begin{align}
\cos((2\pi-\tilde{\omega})k) &= \cos(2\pi k- \tilde{\omega}k)\\
&= \cos(\tilde{\omega}k)\cos(2\pi k) + \sin(\tilde{\omega}k)\sin(2\pi k)\\
&= \cos(\tilde{\omega}k)
\end{align}
つまり,正規化角周波数が\(\pi\)となるような点でサンプリングしたデータの最も高い周波数になり,そこを境に\(2\pi\)になるにしたがってゆっくりとした波になっていく.
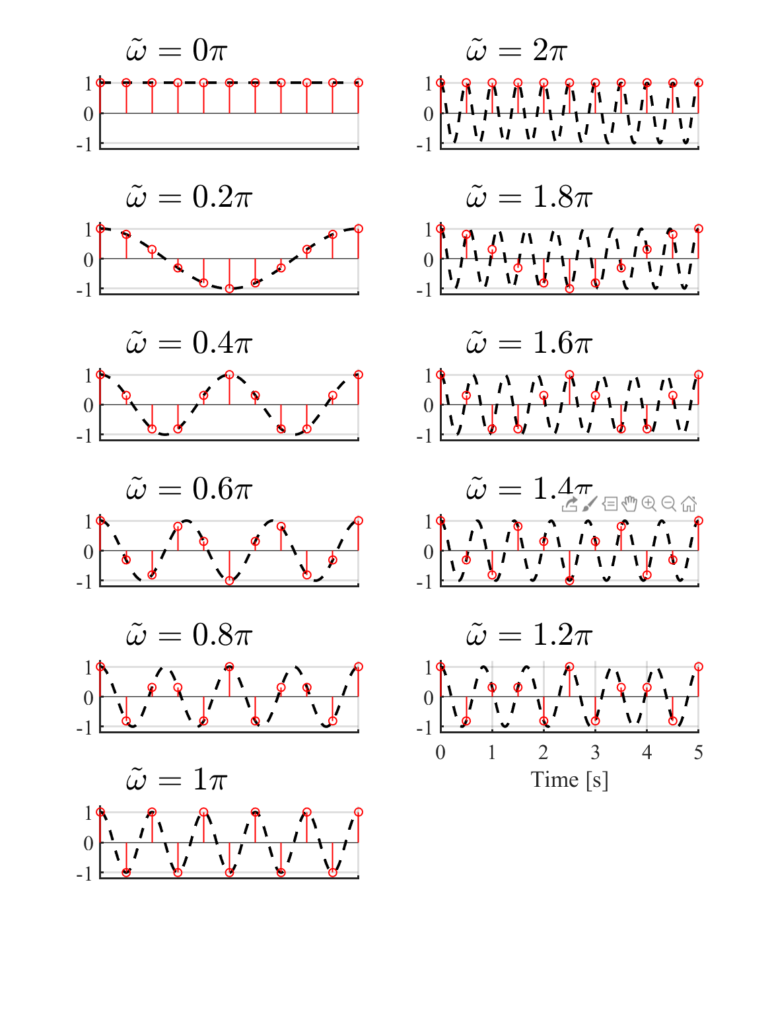
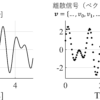
実際に\(\cos(0.2n\pi)\),(ただし\(n=0,1,2,\dots,10\))を図示すると以下のようになる.
図の黒破線はサンプリング前の波,赤丸はサンプリング後のデータ点を表す.
ナイキスト・シャノンのサンプリング定理
上記よりサンプリングした際に,信号がもつ周波数によっては情報が失われる(複数の周波数の成分を区別できない)ことが分かった.
そしてサンプリング周波数\(f_s\)が高いほど,つまりサンプリング間隔\(T_s\)が小さいほどサンプリング後混ざってしまう周波数が現れる間隔が広くなることも予想できる.
ではどれだけ細かくサンプリングすればよいだろうか,例えばあなたのお気に入りの歌をサンプリングして離散データとして保存する際にどのくらいのサンプリング周波数が必要だろうか?
それらを決定するうえで一つの基準となるのがサンプリング定理である.
サンプリング定理はある信号もつ周波数の最大値が\(f_{max}\)のとき,その2倍の周波数\(f_N = 2f_{max}\)のとき,情報を失うことなくサンプリングできるという定理である.
以下でサンプリング定理の感覚的な理解を試みる.
上記の例から正規化角周波数\(\tilde{\omega}=\pi\)を超えると,それよりゆっくりとした波と見分けがつかなくなるのだった.
これを正規化する前の角周波数\(\omega\)や周波数\(f\)で考えると
\begin{align}
\omega &= \frac{\tilde{\omega}}{T_s}\\
f &= \frac{\omega}{2\pi} = \frac{\tilde{\omega}}{2\pi T_s}
\end{align}
より,サンプリング後に情報が失われるか,失われないかの境界が非正規化角周波数では\(\pi /T_s\),周波数では\(\frac{1}{2T_s} = \frac{f_s}{2}\)とサンプリング周波数\(f_s\)の半分になることがわかる.
つまり,サンプリング定理で信号に含まれる最大周波数の2倍以上でサンプリングすればよいというのは様々な波をサンプリングしたときに,全ての波の情報が区別できる条件となっている.
ある信号のもつ周波数の最大値が\(f_{max}\) Hzのときその2倍の周波数をナイキスト周波数とよぶ.
このナイキストというのはスウェーデンの物理学者ハリー・ナイキスト(1889-1976)の名前から来ている.
略歴
ナイキストは1907年にアメリカに移住し,University of North Dakotaでelectrical engineering の学士号(1914),修士号(1915)を取得し,Yale Universityで物理学の博士号を取得した(1917).
卒業後,AT&Tの研究開発部門(のちのベル研究所,Bell Telephone Laboratories)で1954年の定年まで勤めた.
主要な功績
熱雑音,フィードバック増幅器の安定性,通信(FAXやテレビ)に関する重要な研究を行った.
特にナイキストは,単位時間当たりに電信チャネルに通すことができる独立したパルスの数は,チャネルの帯域幅の2倍に制限されることを決定し,その結果をCertain factors affecting telegraph speed (1924)と Certain topics in Telegraph Transmission Theory (1928) という論文で発表した.
この法則は本質的に,現在ナイキスト・シャノンのサンプリング定理として知られているものの双対である.
ハリー・ナイキストの名前が付いた用語(リンクはwikipedia)
- Nyquist rate
- Nyquist frequency
- Nyquist filter
- Nyquist plot
- Nyquist ISI criterion
- Nyquist (programming language)
- Nyquist stability criterion


ディスカッション
コメント一覧
まだ、コメントがありません